सिद्ध कीजिए कि √−1−√−1−√1−......∞ तक =ω या ω2
माना √−1−√−1−√1−......∞ तक
इसलिए x=√1−1x⇒x2=−1−x
⇒ x2+x+1=0
⇒ x=−1±√1−4×1×12×1
=1−±√−32
=−1±√3⋅i2=ω या ω2
Topper's Solved these Questions
- सम्मिश्र संख्याएँBOOK - BALAJI PUBLICATIONCHAPTER - सम्मिश्र संख्याएँEXERCISE - अभ्यास प्रश्न 7.1
16 Videos
- सम्मिश्र संख्याएँBOOK - BALAJI PUBLICATIONCHAPTER - सम्मिश्र संख्याएँEXERCISE - अभ्यास प्रश्न 7.2
10 Videos
- सम्बन्ध एवं फलन BOOK - BALAJI PUBLICATIONCHAPTER - सम्बन्ध एवं फलन EXERCISE - स्वमूल्यांकन परीक्षण
15 Videos
- सरल रेखाएं BOOK - BALAJI PUBLICATIONCHAPTER - सरल रेखाएं EXERCISE - (B ) विवेचनात्मक सोच वाले प्रश्न
3 Videos
Similar Questions
निम्नलिखित संख्याओं को x+iy के रूप में निरूपित कीजिए -
(i) (1+i)(1−2i)1+3i (ii) (12+i)(−23−12i) (iii) 2−3i5−4i (iv) 4+√−34−√−3
View Solutionनिम्नलिखित के वर्गमूल ज्ञात कीजिए -
(i) 354+3i (ii) 9+40i
(iii) 1+i (iv) x2+1x2−4i(x−1x)−6
(v) x2y2+y2x2−1i(xy−yx)−94 (vi) 5+12i
(vii) 2+3i
View Solutionयदि G={7,8} तथा H={5,4,2} है तो G×H एवं H×G ज्ञात कीजिए ।
View Solutiona व b के किस मान के लिए रेखा ax+by+8=0 द्वारा अक्षों पर कटा गया अन्तः खंड रेखा 2x−3y+6=0 द्वारा काटे गए अन्तः खंडो के लम्बाई में बराबर तथा चिन्हो में विपरीत है?
View SolutionIf |z-1|<=2 and | omega z-1-omega^(2)|=a then (a) 0<=a<=2 (b) (1)/(2)<=a<=(sqrt(3))/(2) (c) (sqrt(3))/(2)-(1)/(2)<=a<=(1)/(2)+(sqrt(3))/(2)
View Solution√−1−√−1−√−1∞ is equal to (where ω is the imaginary cube root of unity and i=√−1)
View Solutionthe roots of equation x2−x+1=0 are 1−√3i2and1+√3i2. these are written as −ω,−ω2. how these are -ωand−ω2. kindly explain.
View SolutionThe value of (1+sqrt(omega)+omega)(1-sqrt(omega)+omega)=
View SolutionDifferentiate tan−1(√1+x2−√1−x2√1+x2+√1−x2)w.r.t.sin−1(2x1+x2)
View SolutionProve that x=√−1−√−1−√−1−…→∞=ωorω2
View SolutionFind the tension in each cord in figure-2.48, if the weight of the suspended block is w.
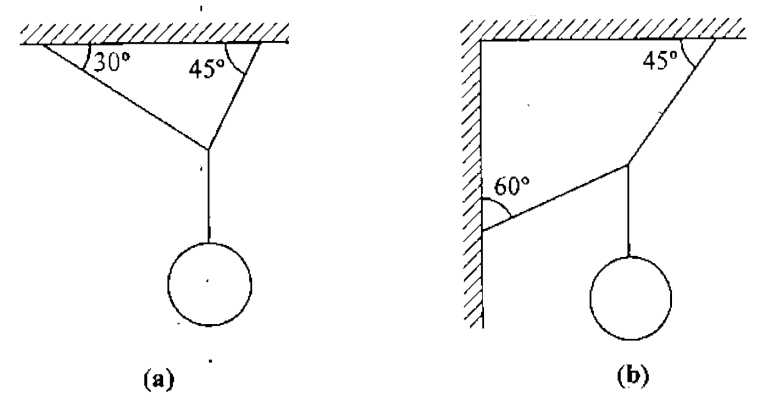
[(a)2w1+√3,√6w1+√3,(b)2w√3−1,√6w√3−1]
View Solutionसाबित कीजिये कि
√−1−√−1−√−1−...to∞=ωorω2
View SolutionIf D1=∣∣ ∣ ∣∣1111ωω21ω2ω∣∣ ∣ ∣∣andD2=∣∣ ∣ ∣∣11ω11ω2ω2ω1∣∣ ∣ ∣∣ show that , D1=√3iD2 where ω=−1+√3i2andi=√−1 .
View Solutionसिद्ध कीजिए की :
√8=1+34+3.54.8+3.5.74.8.12+............. अनंत तक|
View SolutionProve that √−1−√−1−√1−… ∝=worw2 .
View Solution
