यदि Sn=1+q+q2+....+qn
Sn=1+q+12+(q+12)2+...+(q+12)n,q≠1 तब सिद्ध कीजिए कि -
n+1C1+n+1C2S1+n+1C3S2+...+n+1Cn+1Sn=2nSn
Text Solution
स्पष्टतः Sn=1−qn+11−q ...(i)
तथा Sn=1−(q+12)n+11−q+12=2n+1−(q+1)n+12n(1−q) ...(ii)
इसलिए n+1C1+n+1C2⋅S1+n+1C3S2+...+n+1Cn+1Sn
=11−q[n+1C1(1−q)+n+1C2(1−q2)+n+1C3(1−q3)+...+n+1Cn+1(1−qn+1]
=11−q[n+1C1+n+1C2+...+n+1Cn+1]−[n+1C1⋅q+n+1C2⋅q2+...+n+1Cn+1⋅qn+1]
=11−q[(2n+1−1)−{(1+q)n+1−1}]=2n+1−(1+q)n+1(1q)
=2nSn (समीकरण (ii ) से )
|
Topper's Solved these Questions
- द्विपद प्रमेय BOOK - BALAJI PUBLICATIONCHAPTER - द्विपद प्रमेय EXERCISE - अभ्यास प्रश्न 11.1
20 Videos
- द्विपद प्रमेय BOOK - BALAJI PUBLICATIONCHAPTER - द्विपद प्रमेय EXERCISE - अभ्यास प्रश्न 11.2
10 Videos
- द्विघात समीकरण BOOK - BALAJI PUBLICATIONCHAPTER - द्विघात समीकरण EXERCISE - स्वमूल्यांकन परीक्षण ( विवेचनात्मक सोच वाले प्रश्न )
7 Videos
- प्रायिकताBOOK - BALAJI PUBLICATIONCHAPTER - प्रायिकताEXERCISE - NCERT प्रारूप प्रश्न
9 Videos
Knowledge Check
Three charges −q1,+q2 and −q3 are placed as shown in the figure. The x-component of the force on −q1 is proportional to
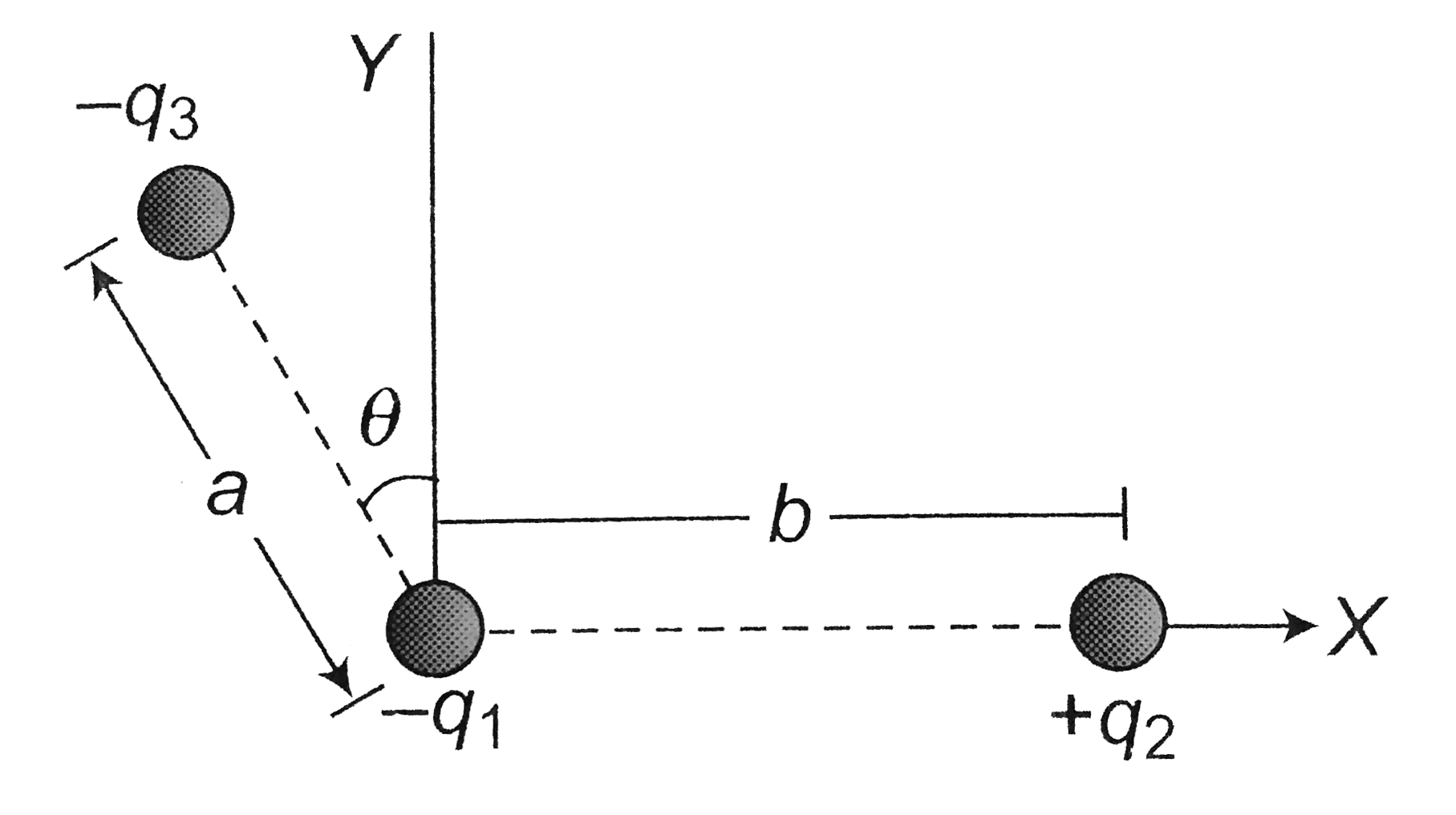 Aq2b2−q3a2sinθBq2b2−q3a2cosθCq2b2+q3a2sinθDq2b2+q3a2cosθ
Aq2b2−q3a2sinθBq2b2−q3a2cosθCq2b2+q3a2sinθDq2b2+q3a2cosθ
