यदि a,b,c,d गुणोत्तर श्रेणी में है, तो सिध्द कीजिए कि-
(a2+ac+c2)(b2+bd+d2)=(ab+bc+cd)2
b=ar,c=ar2,d=ar3
बायाँ पक्ष (a2+a.ar2+a2r4)(a2r2+a2r2+a2r6)=[a2(1+r2+r4)][a2r2(1+r2+r4)]
a4r2(1+r2+r4)2
=(a2r+a2r3+A2r5)2=(a.ar+ar.ar2+ar2.ar3)2
=(ab+bc+cd)2=दायाँपक्ष
Topper's Solved these Questions
- अनुक्रम तथा श्रेणी BOOK - BALAJI PUBLICATIONCHAPTER - अनुक्रम तथा श्रेणी EXERCISE - अभ्यास प्रश्न 12.10
9 Videos
- अनुक्रम तथा श्रेणी BOOK - BALAJI PUBLICATIONCHAPTER - अनुक्रम तथा श्रेणी EXERCISE - अभ्यास प्रश्न 12.11
17 Videos
- अनुक्रम तथा श्रेणी BOOK - BALAJI PUBLICATIONCHAPTER - अनुक्रम तथा श्रेणी EXERCISE - अभ्यास प्रश्न 12.8
6 Videos
- अवकलनBOOK - BALAJI PUBLICATIONCHAPTER - अवकलनEXERCISE - स्वमूल्यांकन परिक्षण
15 Videos
Similar Questions
ज्ञात कीजिए Σ(2n2−3n+5)
View Solutionनिम्नलिखित श्रेणियों के अनन्त पदों का योग ज्ञात कीजिए |
1+2.13+3.132+4.133+…
View Solutionगुणोत्तर श्रेणी के तीन पदों का योग 21 तथा गुणनफल 216 है | संख्याएँ ज्ञात कीजिए |
View Solutionसिद्ध कीजिएः की महत्तम पूर्णांक फलन f(x)=[x],0<x<3,x=1 तथा x=2 पर अवलंकन नहीं है
View SolutionIf abcd=1 where a,b,c,d are positive reals then the minimum value of a^(2)+b^(2)+c^(2)+d^(2)+ab+ac+ad+bc+bd+cd is
View SolutionIf a, b, c, d are in G.P., show that: (ab+bc+cd)2=(a2+b2+c2)(b2+c2+d2)
View SolutionIn the figure, seg AD⊥ side BC and B−D−C, then prove AB2−BD2=AC2−CD2.
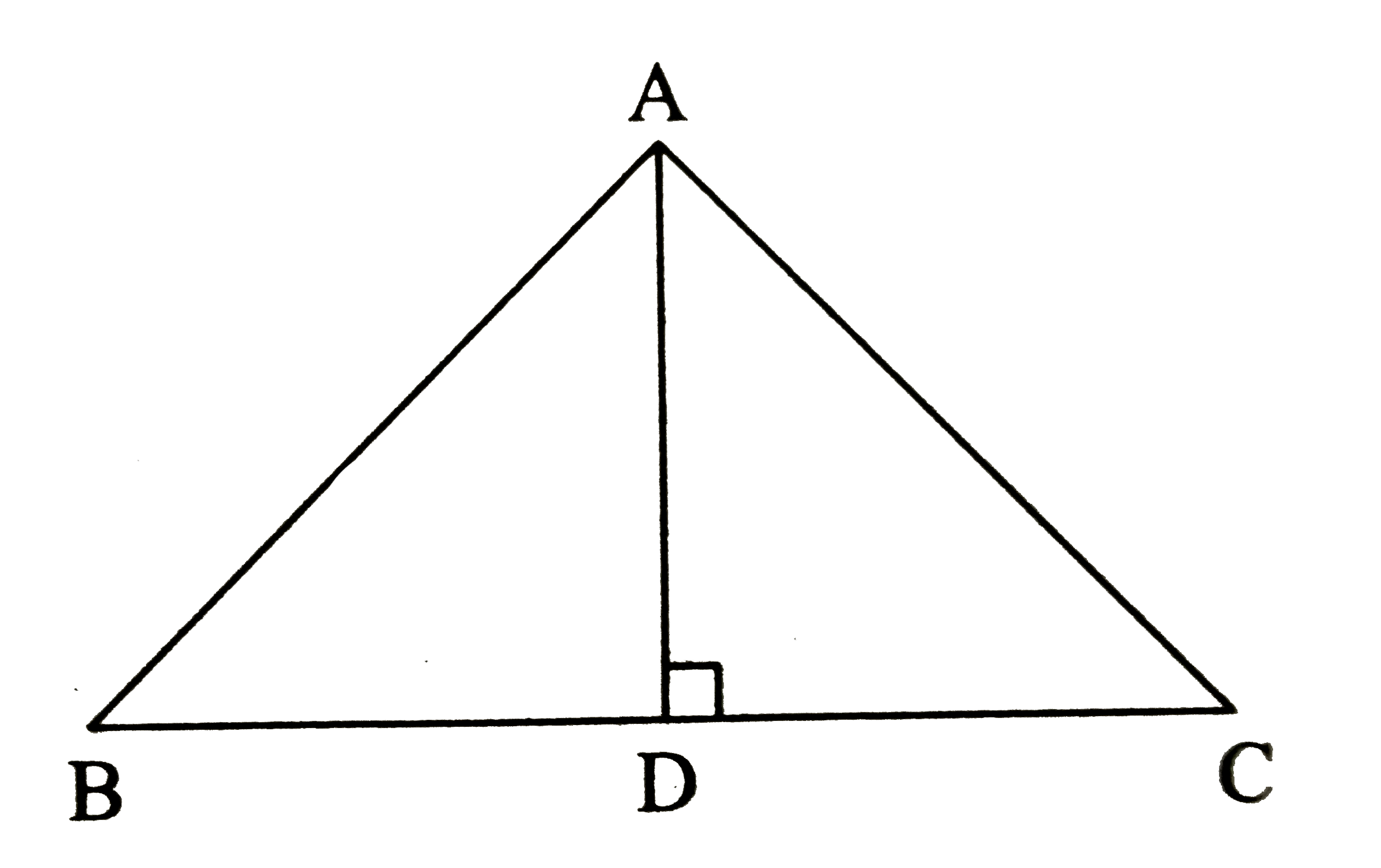
View Solutionसिद्ध कीजिए कि:
∣∣∣ad+bcbd−acac−bdad+bc∣∣∣=(a2+b2)(c2+d2).
View Solutionयदि a,b,c,d गुणोत्तर श्रेढी में हों, तो सिद्ध कीजिए कि :
(b+c)(b+d)=(c+a)(c+d)
View Solutionयदि a,b,c समान्तर और a,b,c+1 गुणोत्तर श्रेणी में हो तो
View SolutionIn adjoining figure, seg AD bot side BC, B-D-C. Prove that AB^(2) + CD^(2) = BD^(2) + AC^(2)
View SolutionIf A, B, C and D are four points in the plane such that |AB|2+|CD|2=|BC|2+|DA|2=100, then AC⋅BD =
View Solutionयदि a:b=c:d हो, तो सिद्ध कीजिए कि
a2+ab+b2c2+cd+d2=a2−ab+b2c2−cd+d2
View SolutionIf a, b, c and d are in G.P. show that (a2+b2+c2)(b2+c2+d2)=(ab+bc+cd)2
View Solutionlf abcd=1 where a,b,c,d are positive reals then the minimum value of a2+b2+c2+d2+ab+ac+ad+bc+bd+cd is
View Solution
