(a) उस वृत्त का समीकरण ज्ञात कीजिए जो मूलबिंदु से होकर जाता है तथा x व y -अक्षों की धनात्मक दिशा से क्रमशः 6 तथा 8 इकाई के अन्तःखण्ड काटता है।
(b) उस वृत्त का समीकरण ज्ञात कीजिए जो मूलबिंदु से गुजरता है और x व y -अक्ष पर धन दिशा में क्रमशः 3 व 4 मात्रक का अन्तःखण्ड काटता है।

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

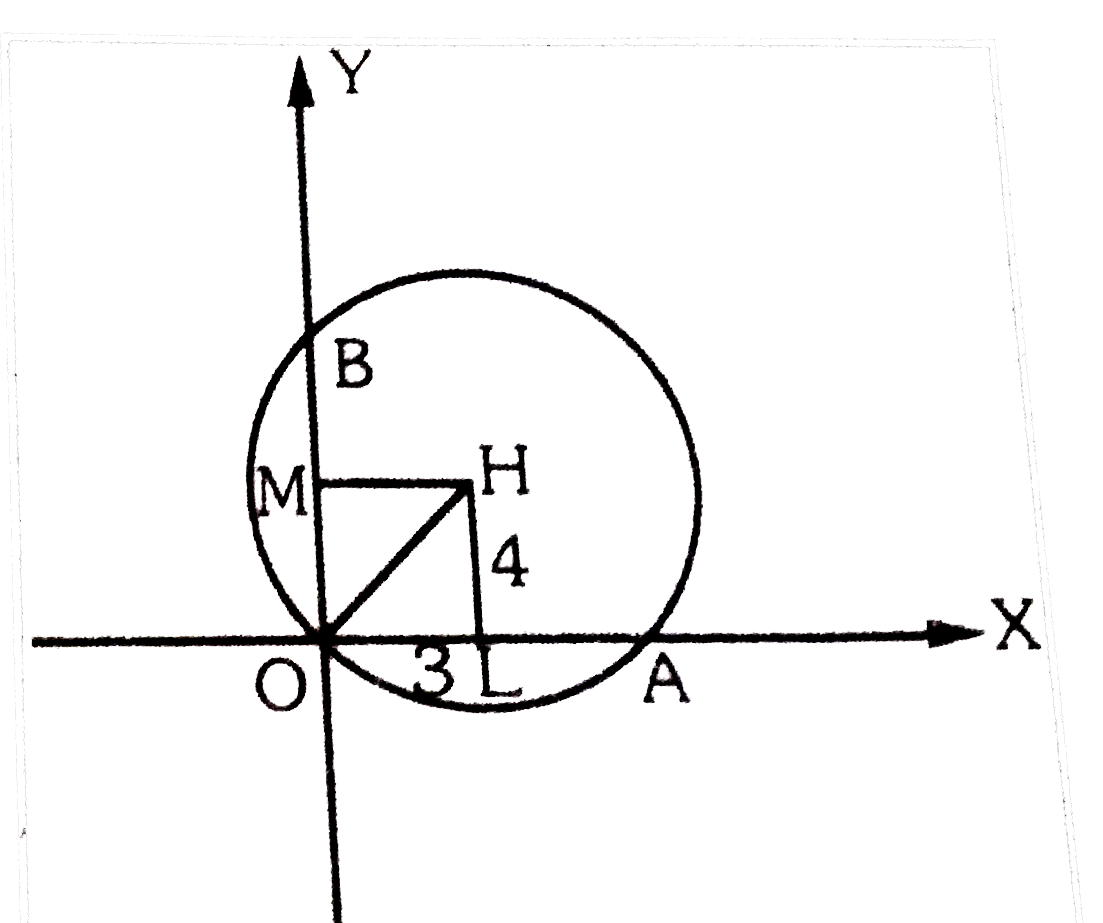
(a) प्रश्नानुसार, OA=6 ⇒ OL=3
OB=8 ⇒ OM=4
⇒LH=4 तथा H≡H(3,4)
अब, वृत्त की त्रिज्या =OH
=√(3−0)2+(4−0)2
=√25=5 इकाई
∴ वृत्त का समीकरण (x−3)2+(y−4)2=(5)2
⇒x2+y2−6x−8y=0,
यही वृत्त का अभीष्ट समीकरण है।
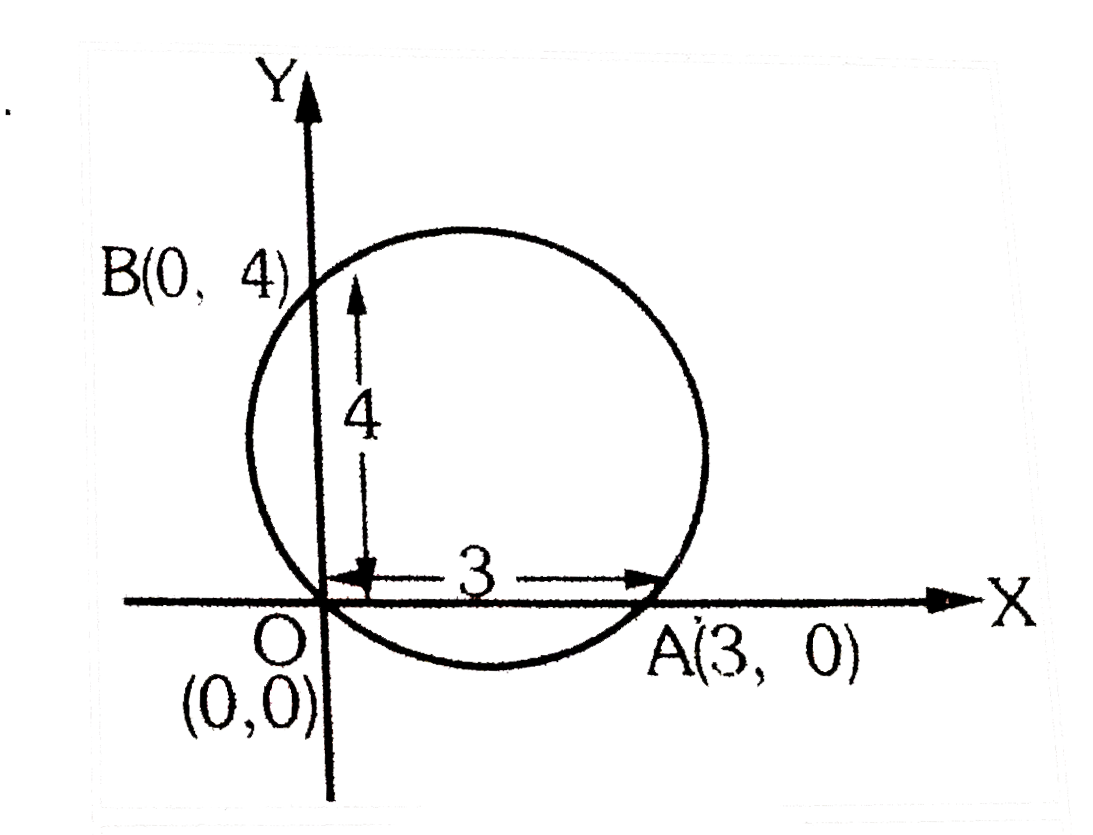
ocr_image
(b) माना वृत्त धन दिशा में x -अक्ष से OA=3 तथा y -अक्ष से OB=4 के अन्तःखण्ड काटता है।
बिंदु A के निर्देशांक =(3,0)
तथा बिंदु B के निर्देशांक =(0,4)
माना वृत्त का समीकरण
x2+y2+2gx+2fy+c=0 ...(i)
∵ वृत्त (i) बिंदु (0,0) से होकर जाता है। अतः
0+0+2g×0+2f×0+c=0
⇒c=0 ...(ii)
इसी प्रकार वृत्त (i) बिंदु (3,0) व (0,4) से भी होकर जाता है इसलिए
(3)2+(0)2+2g(3)+2f(0)+c=0
⇒6g+c=−9 ...(iii)
तथा (0)2+(4)2+2g(0)+2f(4)+c=0
⇒8f+c=−16 ...(iv)
समीकरण (ii), (iii) व (iv) को हल करने पर
g=−32,f=−2,c=0
ये सभी मान समीकरण (1) में रखने पर
x2+y2+2(−32)x+2(−2)y+0=0
⇒x2+y2−3x−4y=0
ocr_image

|
Class 11MATHSCONIC SECTIONS

Topper's Solved these Questions

Similar Questions