उस दीर्घवृत्त का समीकरण ज्ञात कीजिए जो मूलबिंदु से होकर जाता है तथा जिसकी नाभियाँ बिंदुओं (−1,1) तथा (1,1) पर है |
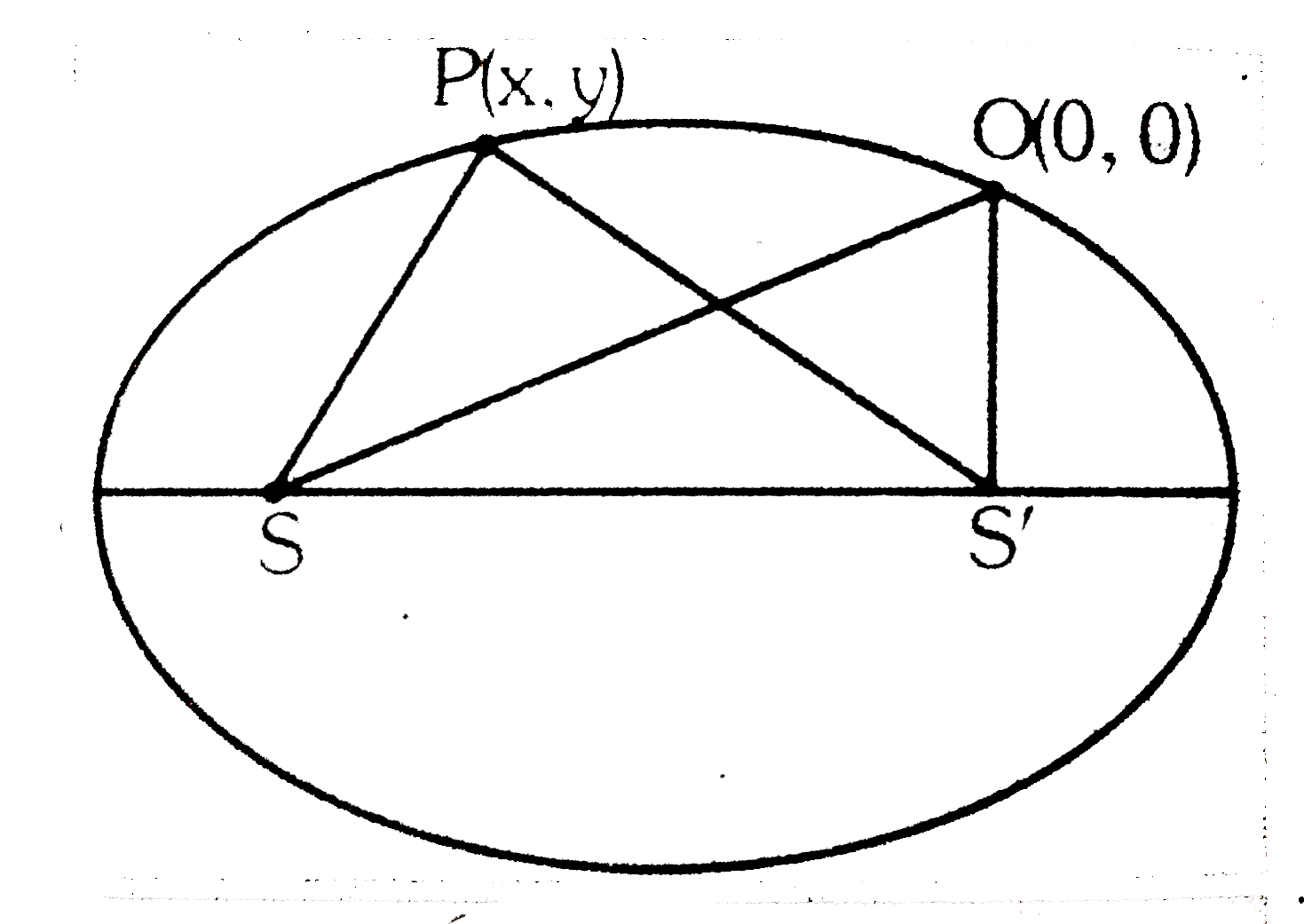
दीर्घवृत्त का नाभियाँ S≡S(−1,1)
व S'≡S'(1,1)
माना बिन्दु P(x,y) दीर्घवृत्त पर स्थित कोई बिन्दु है |
हम जानते है कि दीर्घवृत्त पर स्थित किसी बिन्दु की नाभीय दुरियो का योग अचर होता है |
PS+PS'= अचर =OS+OS'
⇒√(x+1)2+(y−1)2+√(x−1)2+(y−1)2=2√2
⇒√(x+1)2+(y−1)2+2√2−√(x−1)2+(y−1)2
⇒(x+1)2+(y−1)2=8+[(x−1)2+(y−1)2]−4√(x−1)2+(y−1)2
⇒x2+2x+1+y2−2y+1=8+x2−2x+1+y2−2y+1=4√2√(x−1)2+(y−1)2
⇒4x−8=4√2√(x−1)2+(y−1)2
⇒x−2=−√2√(x−1)2+(y−1)2
⇒x2−4x+4=2(x2−2x+1+y2−2y+1)
⇒x2+2y2−4y=0, यही दीर्घवृत्त का अभीष्ट समीकरण है |
Topper's Solved these Questions
- शंकु परच्छेद: दीर्घवृत्तBOOK - BALAJI PUBLICATIONCHAPTER - शंकु परच्छेद: दीर्घवृत्तEXERCISE - अभ्यास प्रश्न 17.1
21 Videos
- शंकु परच्छेद: दीर्घवृत्तBOOK - BALAJI PUBLICATIONCHAPTER - शंकु परच्छेद: दीर्घवृत्तEXERCISE - अतिलघु उत्तरीय प्रश्न
8 Videos
- शंकु परिच्छेद : परवलय BOOK - BALAJI PUBLICATIONCHAPTER - शंकु परिच्छेद : परवलय EXERCISE - स्वमूल्यांकन परीक्षण ((B) विवेचनात्मक सोच वाले प्रश्न )
6 Videos
- शंकु परिच्छेदः अतिपरवलय BOOK - BALAJI PUBLICATIONCHAPTER - शंकु परिच्छेदः अतिपरवलय EXERCISE - स्वमूल्यांकन परीक्षण ((B) विवेचनात्मक सोच वाले प्रश्न )
1 Videos
Similar Questions
उस दीर्घवृत्त का समीकरण ज्ञात कीजिए जिसकी नाभि (6, 7), नियता x+y+2=0 तथा उत्केन्द्रता 1√3 है |
View Solutionउस दीर्घवृत्त का समीकरण ज्ञात कीजिए जिसके शीर्ष (0,±4) तथा नाभियाँ (0,±√7) है |
View Solutionमाना PQ , परवलय y2=4ax कि नाभीय जीवा है , P व Q पर परवलय की स्पर्शिया , रेखा y=2x+a,a>0 पर स्थित एक बिन्दु पर मिलती है , तब सिध्द कीजिये की जीवा PQ की लम्बाई √a है |
View Solutionयदि किसी अतिपरवलय तथा इसके संयुग्मी अतिपरवलय कि उत्केंद्रिताएँ क्रमशः e व e' हो तो सिद्ध किजिये कि 1e2+1e'2=1
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो रेखाओ x=−3 तथा x=5 से समान दूरी पर है ।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए ,जो रेखाये x−y−6=0 तथा 7x−5y=36 के प्रतिच्छेद बिंदु को मूलबिंदु से मिलती है ।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिंदु(1,2) से होकर जाती है जिसके द्वारा अक्षो से बने त्रिभुज का क्षेत्रफल 92 वर्ग इकाई है
View Solutionउस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाओ के समीकरणy=ax,y=bx तथा ax+by+c=0 है
View Solutionउस दीर्घवृत का समीकरण ज्ञात कीजिए जो बिन्दुओ (−3,1) और (2,−2) से होकर जाता है तथा जिसका केंद्र मूलबिंदु पर है । उत्केंद्रता भी ज्ञात कीजिए ।
View Solutionउस समतल का समीकरण ज्ञात कीजिए, जो अक्षों से समान अन्तःखण्ड काटता है तथा बिंदु (2, 3, 4) से होकर जाता है |
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (a,b,c) से होकर जाती है तथा Y-अक्ष के समान्तरहै।
View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionउस सरल रेखा का समीकरण जो रेखाओं 3x-y+ 2 = 0 तथा 5x-2y+ 7 = 0 के प्रतिच्छेद बिन्दु से गुजरती है तथा जिसकी प्रवणता अनन्त है, होगा
View Solution
