सिद्ध कीजिये कि f≡(p∧q)∨(~p)∨(p∧~q) एक पुनरुक्ति है
संयुक्त कथन f के लिए सत्यमान सरणी निम्न होगी
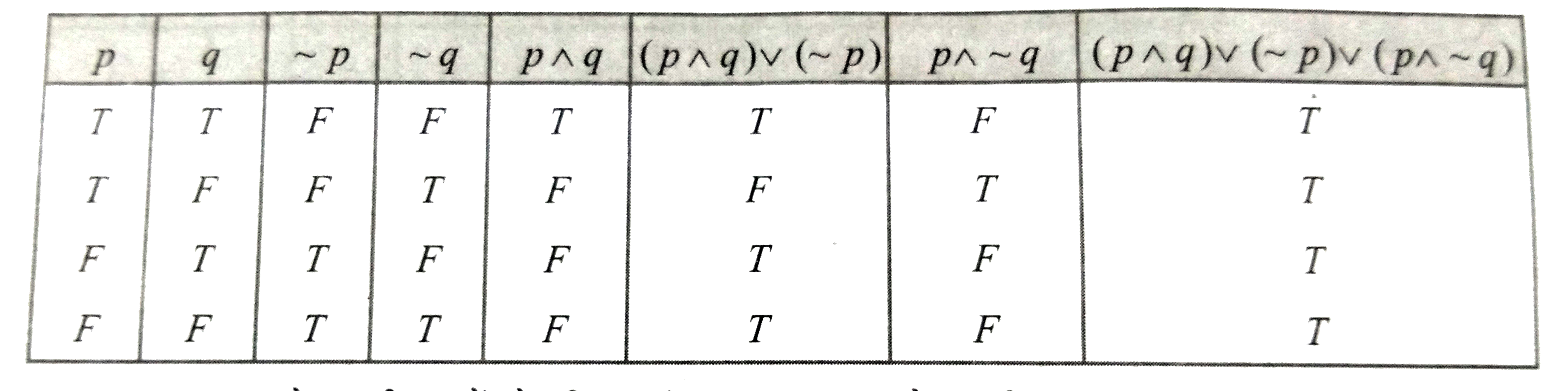
स्पृष्टा p व q के सभी मनो के लिए संयुक्त कथन f के सभी सत्यमान सत्य है इसलिए यह एक (tautology) पुनरुक्ति है
Topper's Solved these Questions
- गणितीय विवेचन BOOK - BALAJI PUBLICATIONCHAPTER - गणितीय विवेचन EXERCISE - विविध उदाहरण
23 Videos
- गणितीय विवेचन BOOK - BALAJI PUBLICATIONCHAPTER - गणितीय विवेचन EXERCISE - अभ्यास प्रश्न 22.1
20 Videos
- गणितीय आगमन का सिद्धांत BOOK - BALAJI PUBLICATIONCHAPTER - गणितीय आगमन का सिद्धांत EXERCISE - विवेचनात्मक सोच वाले प्रश्न
2 Videos
- ज्या तथा कोज्या सूत्र BOOK - BALAJI PUBLICATIONCHAPTER - ज्या तथा कोज्या सूत्र EXERCISE - स्वमूल्यांकन परीक्षण (Self Assessment Test) विवेचनात्मक सोच वाले प्रश्न (Critical Thinking Problems)
9 Videos
Similar Questions
क्या निम्नलिखित वाक्य कथन है अपने उत्तर को कारण सहित लिखिए
8,6 से छोटा है
View Solutionनिम्न वाक्यों में कौन-कौन से वाक्य कथन है
वह एक डॉक्टर है
View Solutionसिद्ध कीजिये की a+ar+ar2+...+aran−1=a(rn−1)r−1,r>1
View SolutioncosAa+cosBb+cosCc=a2+b2+c22abc
View Solutionlet (i) (p∨q)∧(p∨~q),(ii)(p∧q)∧(q∨~q),(iii).(p∨q)∧(p∨~q),(iv)(p∨q)∨(p∧~q) then which one is tautology
View SolutionShow that (p∧q)∨(~p)∨(p∧~q) is a tautology
View SolutionLet p and q be two statements, then (p∨q)∨~p is
View SolutionSimplify (p∨q)∧(p∨~q).
View SolutionWrite the duals of the following statements : (i) [~(p∨q)]∧[p∨{~q∧~s)}] ~p∨[(~q)∨(p∨~q)∨~r]
View SolutionThe Bolean Expression (p∧~q)∨q∨(~p∧q∨(~p∧q) is equivalent to
View SolutionThe proposition ~(p∨~q)∨~(p∨q) is logically equivalent to
View SolutionProve that the statements [(~p)∨q]∧[p∨(~r)]∧[(~p)∨(~q)] and ~(p∨r) are logicaly equivalent.
View SolutionThe proposition ~(p∨~q)∨~(p∨q) is logically equivalent to
View SolutionObserve the following statements
I : The dual of [~p∧q)]∨[p∧{~(q∨~s)}] is [~(p∨q)]∧[p∨{~(q∧~s)}]
II : The dual of ~p∧[(~q)∧(p∨q)∧~r] is ~p∨[~q)∨(p∧q)∨~r]
The true statements in the above is/are :
View SolutionShow that (p∧q)∨(~p)∨(p∧~q) is a tautology
View Solution
