एक 14 मी. दौड़ने का पथ दो 120 मी. लम्बे सीधे भागों तथा दो 35 मी. आन्तरिक त्रिज्या वाले अर्धवृत्ताकार भागों से मिलकर बना है | छायांकित भाग के क्षेत्रफल की गणना कीजिए |
दिया है : OB=O'C=35 मी. तथा AB = CD = 14 मी.
∴ OA=O'D=(35+14) मी. = 49 मी.
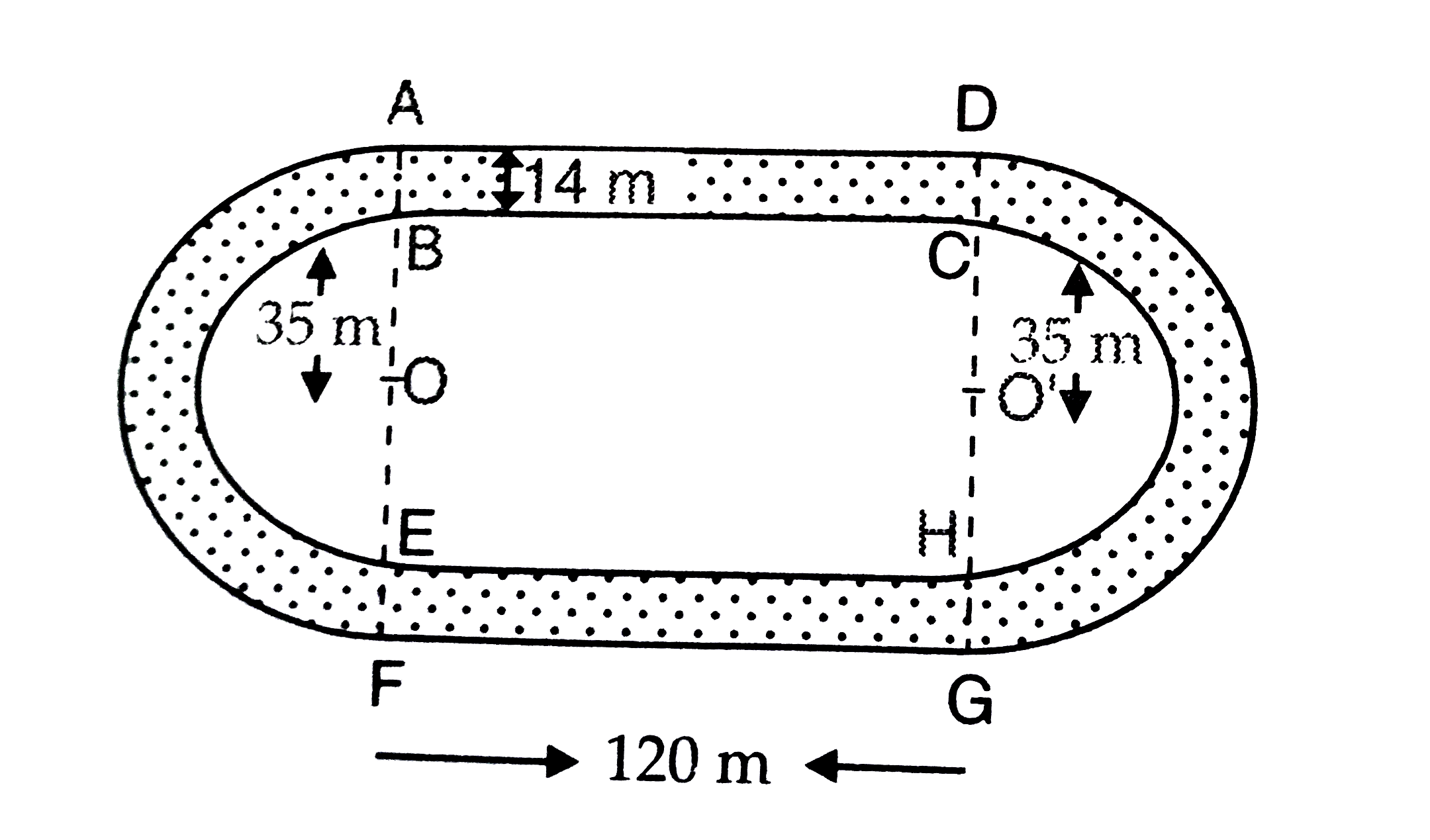
अब, छायांकित भाग का क्षेत्रफल
= आयत ABCD का क्षेत्रफल + आयत EFGH का क्षेत्रफल
+ 2(49 मी. त्रिज्या वाले अर्धवृत्त का क्षेत्रफल)
-2(35 मी. त्रिज्या वाले अर्धवृत्त का क्षेत्रफल)
=(14×20)+(14×20)+2{12×227×(49)2}−2{12×227×(35)2}
{1680+1680+227(492−352)} मी.2
={3360+227(49+35)(49−35)} मी.2
={3360+227×84×14} मी.2
={3360+44×84} मी.2=7056 मी.2
अत: छायांकित भाग का क्षेत्रफल 7056 मी.2 है |
Topper's Solved these Questions
- BOOK - RD SHARMACHAPTER - वृत्तों से सम्बन्धित क्षेत्रफल EXERCISE - प्रश्नावली 15.119videos
वृत्तों से सम्बन्धित क्षेत्रफल
- BOOK - RD SHARMACHAPTER - वृत्तों से सम्बन्धित क्षेत्रफल EXERCISE - प्रश्नावली 15.226videos
वृत्तों से सम्बन्धित क्षेत्रफल
- BOOK - RD SHARMACHAPTER - वृत्त EXERCISE - बहु विकल्पीय प्रश्न15videos
वृत्त
- BOOK - RD SHARMACHAPTER - समान्तर श्रेढ़ी EXERCISE - बहु विकल्पीय प्रश्न35videos
समान्तर श्रेढ़ी
Similar Questions
4.2 सेमी. त्रिज्या वाले वृत्त की परिधि और क्षेत्रफल ज्ञात कीजिए |
08:17View Solution4 सेमी. त्रिज्या वाले वृत्त के केन्द्र पर 30∘ का कोण आन्तरित करने वाली चाप की लम्बाई π के पदों में ज्ञात कीजिए |
07:40View Solutionएक 5 सेमी त्रिज्या वाले वृत्त बिंदु पर स्पर्श रेखा PQ वृत्त के केंद्र O से जाने वाली रेखा को Q पर इस प्रकार काटती है कि OQ=12 सेमी है। PQ=
07:12View Solutionयदि एक समांतर श्रेढ़ी का 7 वाँ तथा 13 वाँ पद क्रमश : 34 तथा 64 है , तो इसका 18 वाँ पद है :
05:14View Solutionपृथ्वी की त्रिज्या 6.4×106 मी है। पृथ्वी-तल से 800 किमी की ऊँचाई पर गुरुत्वीय विभव तथा गुरुत्वीय क्षेत्र की तीव्रता ज्ञात कीजिए। (g=10 मी/से.2)
03:31View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
01:22View Solutionएक समान्तर चतुर्भुज की दो आसान भुजाएँ 2ˆi−4ˆj−5ˆk और 2ˆi+2ˆj+3ˆk है । इसके दोनों विकणों के समान्तर दो मात्रक सदिश ज्ञात कीजिए। विकणों के सदिशों का प्रयोग करके समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
04:07View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
01:15View Solutionकिसी बेलन का अर्धव्यास 2 मी/से की दर से बढ़ता है और ऊँचाई 3 मी/से की दर से घटती है। जब उसकी ऊँचाई 5 मी और अर्धव्यास 3 मी हो, तो बेलन के आयतन के परिवर्तन की दर होगी
34:41View Solutionयदि बेलन का व्यास 20 से. मी. है, तो उसकी त्रिज्या होगी
04:26View Solutionएक धातु के बेलन को, जिसका व्यास 8 से.मी. और ऊँचाई 90 से. मी. है, गलाकर 12 से. मी. व्यास वाले कितने गोले बनाए जा सकते हैं ?
03:17View Solutionयदि गोले का व्यास 14 से. मी. है, तो उसकी त्रिज्या होगी-
02:56View SolutionRevision |दो विशेष त्रिभुज : समबाहु तथा समद्विबाहु #!#एक त्रिभुज की दो भुजाओं की मापों का योग
00:47View SolutionThe distance between two pillars is 120 metres. The height of one pillar is thrice the other. The angles of elevation of their tops from the midpoint of the line connecting their feet are complementary to each other. The height (in metres) of the taller pillar is (Use : sqrt3 =1.732 ) दो खंभो के बीच की दूरी 120 मी. है। एक खंभे को ऊँचाई दूसरे से तिगुणी है। दोनों खंभो के आधार बिंदुओ को मिलाने वाली रेखा के मध्य बिंदू से उनके शीषों के उन्नयन कोण एक दूसरे के पूरक है। बड़े खंभे की ऊँचाई (मी. में) बताएं । (प्रयोग करे: sqrt3 =1.732 )
02:09View SolutionTwo sides of a plots measuring 32 m and 24 m and the angle between them is a perfect right angle. The other two sides measure 25 m each. and the other three angles are not right angles. The area of the plot in m^2 is - एक भूखण्ड की दो भुजाएँ 32 मी. और 24 मी. की हैं और उनके बीच का कोण पूर्ण समकोण है । अन्य दो भुजाएँ प्रति 25 मी. की हैं और अन्य तीन कोण समकोण नहीं हैं । भूखण्ड का क्षेत्रफल ( मी^2 ) में कितना होगा ?
03:25View SolutionA ditch of radius 3.5 m is dug 16 m deep. The earth removed is spread over an area of 400 m^2 to form a platform. Height of the platform is _____. 16 मी गहरी तथा 3.5 मी त्रिज्या वाली एक खाई खोदी जाती है ओर निकाली गई मिट्टी का क्षेत्रफल 400 मी^2 वाला एक प्लेटफार्म तैयार किया जाता था। प्लेटफार्म की ऊँचाई है।
01:48View Solution

