Consider f:{1,2,3}→{a,b,c}and g:{a,b,c}→{apple,ball,cat}defined as f(1)=a, f(2)=b, f(3)=c, g(a)=apple,g(b)=ballandg(c)=cat. Show that f,gandgof are invertible .Find out f−1,g−1 and (gof)−1 and show that (gof)−1=f−1og−1
Given as f={(1,a), (2,b),(c,3)} and g = {(a, apple), (b,ball),(c,cat)}.
Clearly, f and g are bijections.
∴ f and g are invertible.
Then, f−1={(a,1),(b,2),(3,c)} and g−1 = {(apple, a), (ball,b),(cat,c)}
∴ f−1og−1= {apple, 1), (ball,2),(cat,3)} …(1)
f:{1,2,3,}→{a,b,c} and g:{a,b,c} → {apple, ball, cat}
∴ gof:{1,2,3} → {apple, ball, cat}
⇒ (gof(1))=g(f(1))=g(a) = apple
(gof)(2)=g(f(2))=g(b) = ball
And (gof)(3)=g(f(3))=g(c) = cat
∴ gof = {(1, apple), (2,ball),(3,cat)}
Clearly, gof is a bijection.
∴ gof is invertible.
(gof)−1 = {(apple, 1), (ball,2),(cat,3)} ...(2)
Form equations (1) and (2), we get
(gof)−1=f−1og−1
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 1.413videos
RELATIONS AND FUNCTIONS
- BOOK - NCERTCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 1.212videos
RELATIONS AND FUNCTIONS
- BOOK - NCERTCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 1.314videos
RELATIONS AND FUNCTIONS
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - EXERCISE 13.218videos
PROBABILITY
- BOOK - NCERTCHAPTER - SETSEXERCISE - EXERCISE 1.31videos
SETS
Similar Questions
Consider as f(1)=a,f(2)=b,f(3)=c,
g:[a,b,c]→ {apple, ball, cat}
Defined as f(1)=a,f(2)=b,f(3)=c,
g(a) = apple, g(b) = ball, g(c ) = cat
Show that f, g and gof are invertible.
Find f−1,g−1 and (gof)−1 and show that :
(gof)−1=f−1og−1.View SolutionConsider f:{1,2,3}→{a,b,c}and g:{a,b,c}→{apple,ball,cat}defined as f(1)=a, f(2)=b, f(3)=c, g(a)=apple,g(b)=ballandg(c)=cat. Show that f,gandgof are invertible .Find out f−1,g−1 and (gof)−1 and show that (gof)−1=f−1og−1
View Solution
Knowledge Check
- Question 1 - Select One
If A={a,b,c,e,f},B={c,d,e,g}andC={b,c,f,g}. Then, A−(B∩C) is equal to
A{a,b,d,e}B{a,b,e,f}CϕDNone of these - Question 2 - Select One
If f:A→B and g:B→C be the bijective function, then (gof)−1 is:
Af−1og−1BfogCg−1of−1Dgof - Question 3 - Select One
If a,b,c are in H.P, b,c,d are in G.P and c,d,e are in A.P. , then the value of e is
Aab2(2a−b)2Ba2b(2a−b)2Ca2b2(2a−b)2DNone of these
Let f and g be two functions such that gof=IA and fog=IB. Then; f and g are bijections and g=f−1
View Solution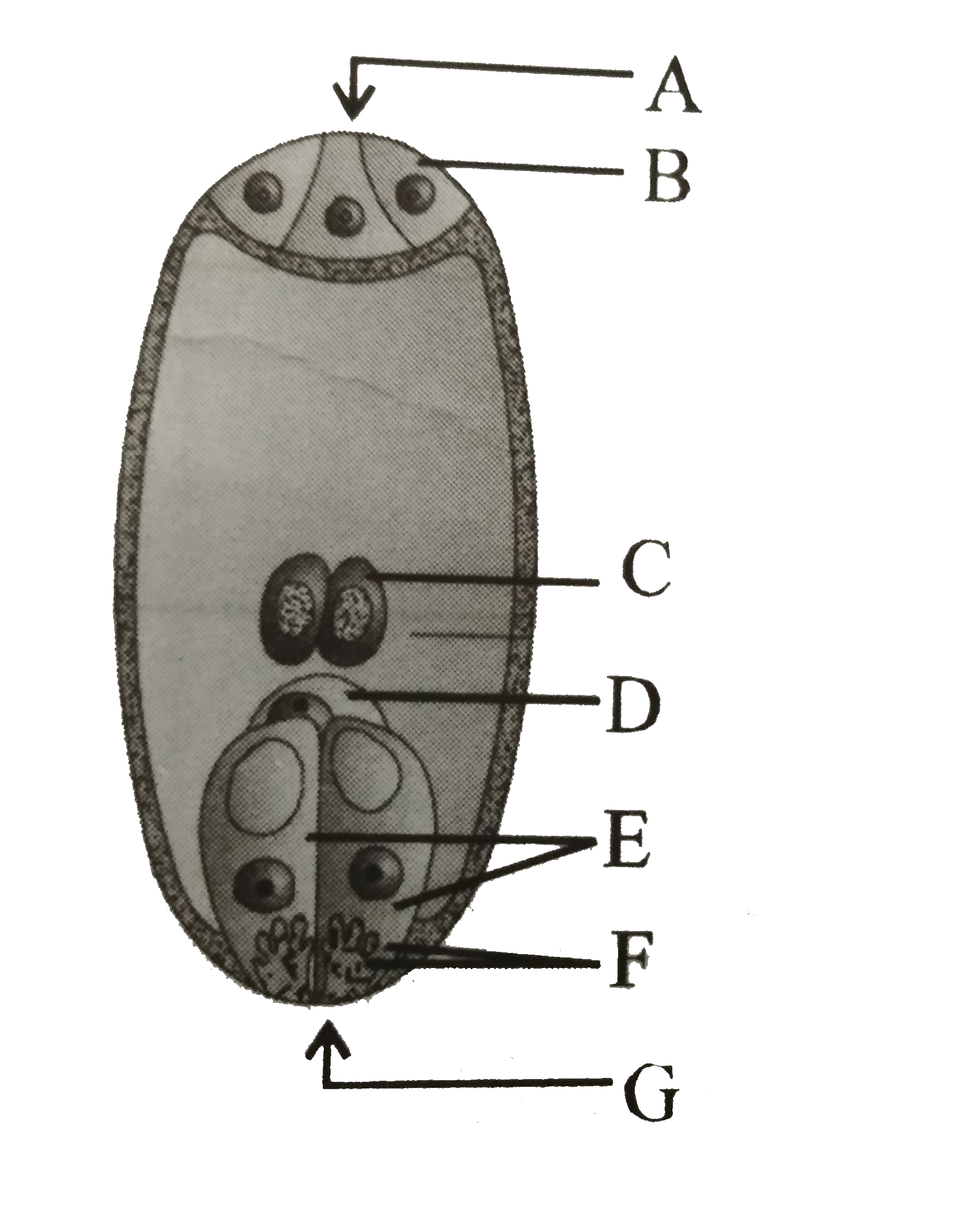
Identify A, B, C, D, E, F,GView SolutionIf a,b,(c+1) are in G.P. and a=(b−c)2 then a,b,c are in
View SolutionConsider function f:A→Bandg:B→C(A,B,⊆R) such that (gof)−1 exists then
View SolutionIf the function f(x):A→B and g(x):B→C are defined such that (g(f(x)))−1 exist then f(x)andg(x) are
View Solution

