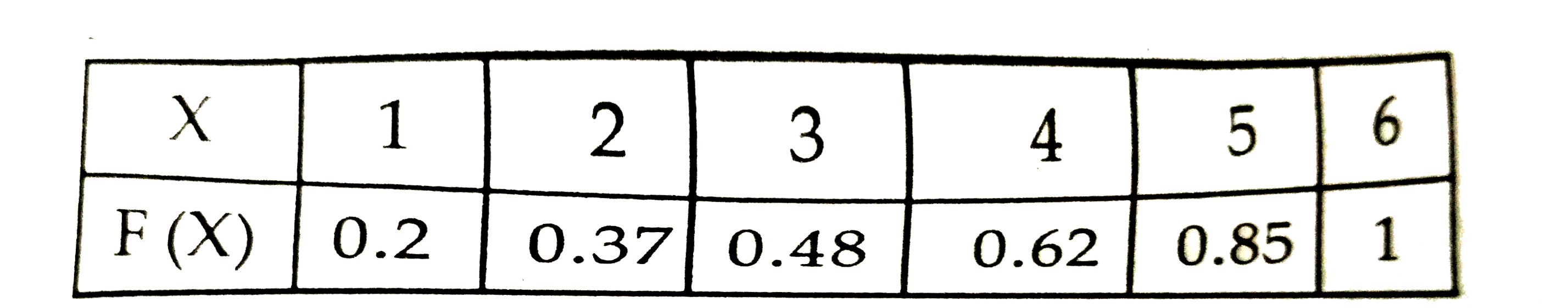For the following distribution function of a r.v X
The correct Answer is:B
To find the probability P(3<X≤5) from the given distribution function F(x), we need to follow these steps:
Step 1: Understand the given distribution function
The distribution function F(x) is given as:
- F(1)=0.2
- F(2)=0.37
- F(3)=0.48
- F(4)=0.62
- F(5)=0.85
- F(6)=1
Step 2: Calculate the probabilities for each value of X
To find the probability P(X=x) for each value of X, we can use the differences between the cumulative probabilities:
- P(X=1)=F(1)=0.2
- P(X=2)=F(2)−F(1)=0.37−0.2=0.17
- P(X=3)=F(3)−F(2)=0.48−0.37=0.11
- P(X=4)=F(4)−F(3)=0.62−0.48=0.14
- P(X=5)=F(5)−F(4)=0.85−0.62=0.23
- P(X=6)=F(6)−F(5)=1−0.85=0.15
Step 3: Identify the relevant probabilities for P(3<X≤5)
The probability P(3<X≤5) includes the values of X=4 and X=5:
- P(X=4)=0.14
- P(X=5)=0.23
Step 4: Calculate the total probability
Now, we add the probabilities of X=4 and X=5:
P(3<X≤5)=P(X=4)+P(X=5)=0.14+0.23=0.37
Final Answer
Thus, the probability P(3<X≤5) is 0.37.
---
The distribution function F(x) is given as:
- F(1)=0.2
- F(2)=0.37
- F(3)=0.48
- F(4)=0.62
- F(5)=0.85
- F(6)=1
To find the probability P(X=x) for each value of X, we can use the differences between the cumulative probabilities:
- P(X=1)=F(1)=0.2
- P(X=2)=F(2)−F(1)=0.37−0.2=0.17
- P(X=3)=F(3)−F(2)=0.48−0.37=0.11
- P(X=4)=F(4)−F(3)=0.62−0.48=0.14
- P(X=5)=F(5)−F(4)=0.85−0.62=0.23
- P(X=6)=F(6)−F(5)=1−0.85=0.15
The probability P(3<X≤5) includes the values of X=4 and X=5:
- P(X=4)=0.14
- P(X=5)=0.23
Now, we add the probabilities of X=4 and X=5:
P(3<X≤5)=P(X=4)+P(X=5)=0.14+0.23=0.37
Thus, the probability P(3<X≤5) is 0.37.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
For the followinng distribution function F(x) of a rv.X.
x123456F(x)0.20.370.480.620.851
P(3<x≤5)=A0.48B0.37C0.27D1.47 - Question 2 - Select One
The points of discontinuity of the function
f(x)=⎧⎪⎨⎪⎩3x+1,0≤x<24x−1,2<x≤65x+2,6<x≤10are:A6B2C6, 2D6, 2, 0 - Question 3 - Select One
Which of the following statement is true for the function f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩√x,x≥1x3,0≤x<1x33−4x,x<0
AIt is monotonic increasing ∀x∈RBf'(x) fails to exist for 3 distinct real values of xCf'(x) changes its sign twice as x varies from (−∞,∞)DFunction attains its extreme values at x1andx2 , such that x1x2>0
Discuss the continuity of the function f, where f is defined by f(x)⎧⎪⎨⎪⎩3,if0≤x≤14,if1<x<35,if3≤x≤10
View SolutionLet f:[0,1]→R (the set of all real numbers) be a function. Suppose the function f is twice differentiable, f(0)=f(1)=0 and satisfies f''(x)−2f'(x)+f(x)≥ex,x∈[0,1]If the function e−xf(x) assumes its minimum in the interval [0,1] at x=14, which of the following is true? (A) f'(x)<f(x),14<x<34 (B) f'(x)>f(x),0<x<14(C)f'(x)<f(x),0<x<14 (D) f'(x)<f(x),34<x<1
View SolutionExpress each of the following sts as an interval :
(i)A={x:x∈R,−4,<x<0}
(ii)B={x:x∈R,0≤x<3}
(iii)C={x:x∈R,2<x≤6}
(iv)D={x:x∈R,−5≤x≤2}
(v)E={x:x∈R,−3≤x<2)
(vi)F={x:x∈R,−2,≤x<0}View SolutionIf a function f(x) is defined as f(x)=⎧⎪⎨⎪⎩−x,x<0x2,0≤x≤1x2−x+1,x>1 then
View SolutionThe p.d.f. of a r.v. X is f(x)={0.5x,0<x<20, otherwise, then P(X≤1) =
View Solution