Poiseuille's's law for the flow of a liquid in a capillary tube is given by
η=πΔPa48LV
where η = co-efficient of viscosity of a liquid ΔP = Pressure difference across a length (L) of a tube of radius (a)
and V = Volume of the liquid flowing per second The maximum error that enters the calculations of η is due to the measurement of
L
a
ΔP
V
The correct Answer is:b
Maximum error is introduced in the total error, in the measurement of the radius (a), as we have to consider (a4), the fourth power of a.
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - MEASUREMENTS EXERCISE - TEST YOUR GRASP10videos
MEASUREMENTS
- BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETISMEXERCISE - TEST YOUR GRASP10videos
MAGNETISM
- BOOK - MARVEL PUBLICATIONCHAPTER - RAY OPTICS (MIRRORS, LENSES AND OPTICAL INSTRUMENTS)EXERCISE - TEST YOUR GRASP10videos
RAY OPTICS (MIRRORS, LENSES AND OPTICAL INSTRUMENTS)
Similar Questions
The critical velocity of the flow of a liquid through a pipe of radius 3 is given by vc=(Kηrp), where p is the density and η, is the coefficient of viscosity of liquid. Check if this relation is dimentionally correct.
View SolutionThe rate flow (V) of a liquid through a pipe of radius (r ) under a pressure gradient (P//I) is given by V=π8PR4Iη, Where η is coefficient of visocity of the liquied. Check whether the formula is correct or not.
View Solution
Knowledge Check
- Question 1 - Select One
A liquid of coefficient of viscosity η is flowing steadily through a capillary tube of radius r and length I. If V is volume of liquid flowing per sec. the pressure difference P at the end of tube is given by
AP=8πIVηr4BP=8ηr4IπVCP=8ηIVπr4DP=8ηr4VπI - Question 2 - Select One
The rate of flow of liquid ina tube of radius r, length l, whose ends are maintained at a pressure difference P is V=πQPr4ηl where η is coefficient of the viscosity and Q is
A8B18C16D116 - Question 3 - Select One
When a liquid moves steadily under some pressure through a horizontal tube, it moves in the form of cylindrical layers coaxial to the ends of the tube. The velocity of different layers is different. The velocity of the layer is maximum along the axis of the tube and it decreases as one moves towards the walls of the tube. According to Poiseuille, the rate of flow of liquid through a horizontal capillary tube varies as the relation Vαpr4ηl where l and r are the length and radius of the tube and p is the pressure different between the ends of the tube and is the constant of proportionality.
When two capillary tubes through which the liquid is flowing are joined in series then the equivalent liquid resistance isARs=R1+R2BRs=R1−R2C1Rs=1R1+1R2DKηpr=1R1−1R2
Three capillaries of lengths l1,l2 and l3 and radii r1,r2 and r3 respectively are joined in series. If p is pressure difference across the combination of capallaries, what will be the volume of liquid flowing per second?
View SolutionA liquid flows through two capillary tubes A and B connected in series. The length and radius of B are twice that of A. What is the ratio of the pressure difference across A to that across B ?
View SolutionA vertical steel rod has radius a. The rod has a coat of a liquid film on it. The liquid slides under gravity. It was found that the speed of liquid layer at radius r is given by
v=ρgb22ηln(ra)−ρg4η(r2−a2)
Where b is the outer radius of liquid film, η is coefficient of viscosity and ρ is density of the liquid.
(i) Calculate the force on unit length of the rod due to the viscous liquid?
(ii) Set up the integral to calculate the volume flow rate of the liquid down the rod. [you may not evaluate the integral]
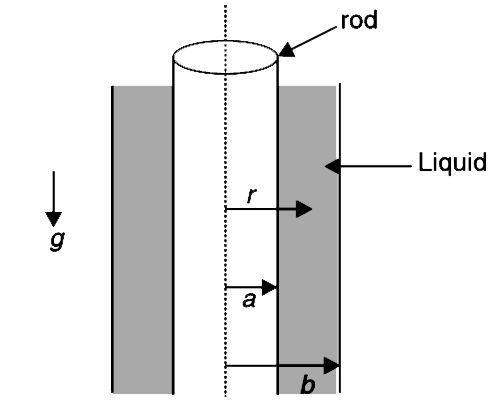 View Solution
View SolutionIf l is length of the tube and r is the radius of the tube, then the rate of volume flow of a liquid is maximum for the following measurements. Under the same pressure difference.
View SolutionThe volume of a liquid of density ρ and viscosity η flowing in time t through a capillary tube of length l and radius R, with a pressure difference P, across its ends is proportional to :
View Solution

