When light of wavelength travels through glass, the refractive index of glass varies with wavelength as . What are the dimensional formulae of A and B?
The correct Answer is:c
Thus is a dimensionless quantity
or .
As all terms should have the same dimensions
For
and
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - MEASUREMENTS EXERCISE - TEST YOUR GRASP10videos
MEASUREMENTS
- BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETISMEXERCISE - TEST YOUR GRASP10videos
MAGNETISM
- BOOK - MARVEL PUBLICATIONCHAPTER - RAY OPTICS (MIRRORS, LENSES AND OPTICAL INSTRUMENTS)EXERCISE - TEST YOUR GRASP10videos
RAY OPTICS (MIRRORS, LENSES AND OPTICAL INSTRUMENTS)
Similar Questions
The refractive index μ of a medium is found to vary with wavelength λ as μ=A+Bλ2. What are the dimensions of A and B?
View SolutionWhen white light travels through glass, the refractive index of glass (μ=velocity of light in air/velocity of light in glass) is found to vary with wavelength as μ=A+Bλ2. Using the principle of homogeneity of dimensions, Find the SI units in which the constants A and B expressed.
View Solution
Knowledge Check
- Question 1 - Select One
The angles of incidence and refraction of a monochromatic ray of light of wavelength λ at an air-glass interface are i and r, respectively. A parallel beam of light with a small spread δλ in wavelength about a mean wavelength λ is refracted at the same air-glass interface. The refractive index μ of glass depends on the wavelength λ as μ(λ)=a+b/λ2 where a and b are constants. Then the angular spread in the angle of refraction of the beam is
A∣∣∣siniλ3cosrδλ∣∣∣B∣∣∣2bλ3δλ∣∣∣C∣∣∣2btanraλ3+bλδλ∣∣∣D∣∣ ∣∣2b(a+b/λ2)siniλ3δλ∣∣ ∣∣ - Question 2 - Select One
Monochromatic light to wavelength 6000Å travels through glass of refractive index 32. The distance travelled by the wavefront 1 picosecond is
A100μmB200μmC300μmD400μm - Question 3 - Select One
The correct curve between refractive index μ and wavelength λ will be
 A
A B
B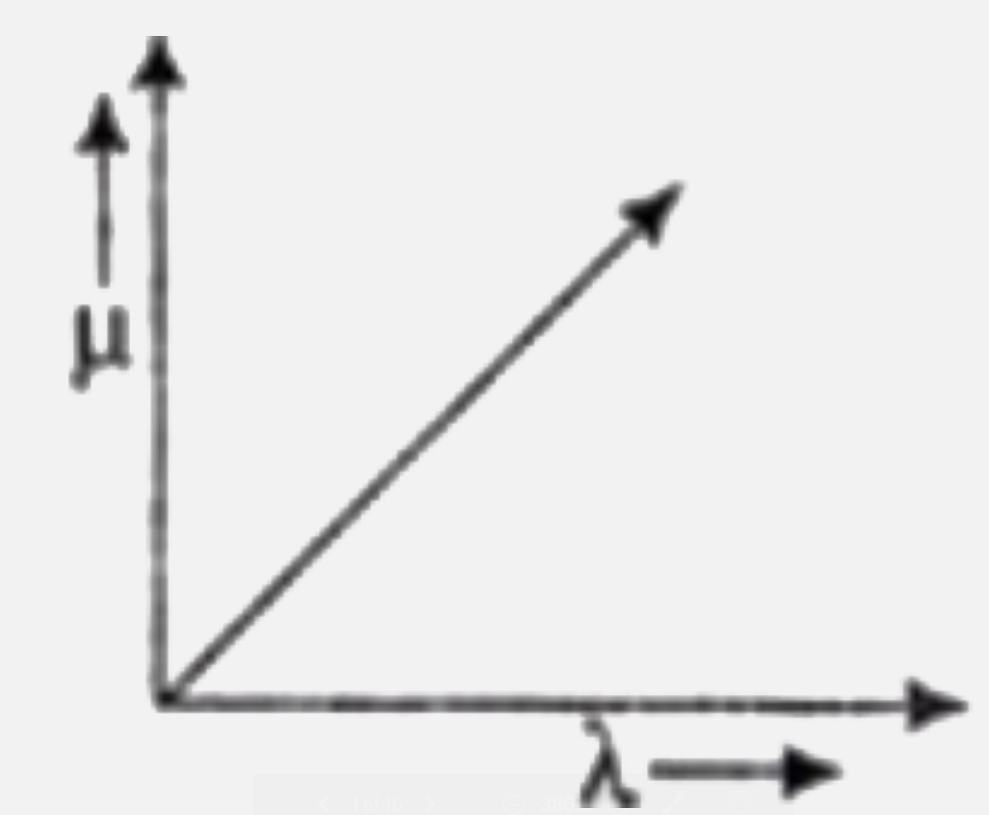 C
C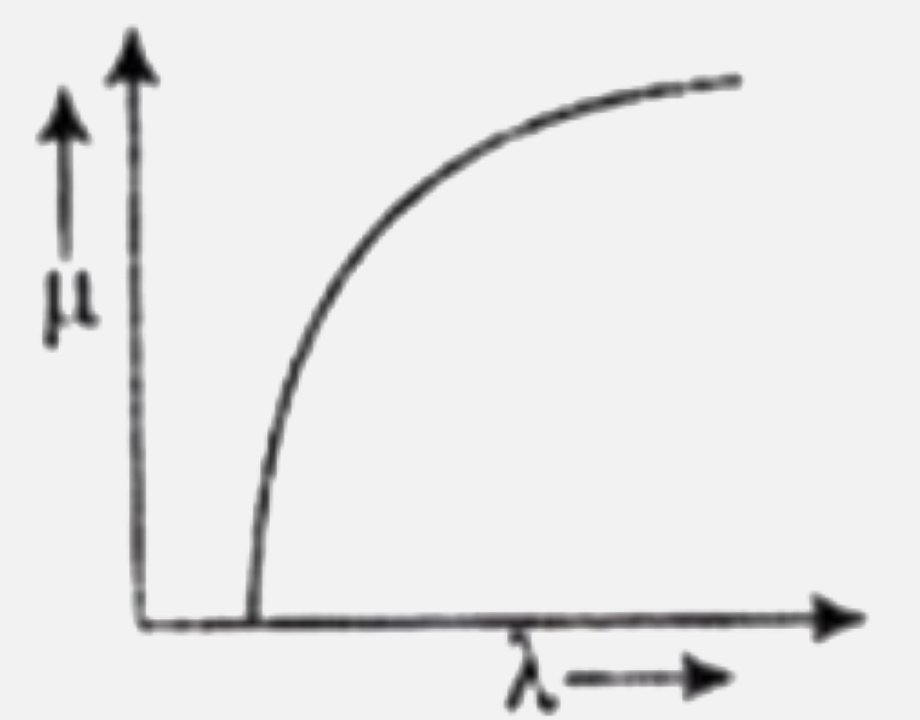 D
D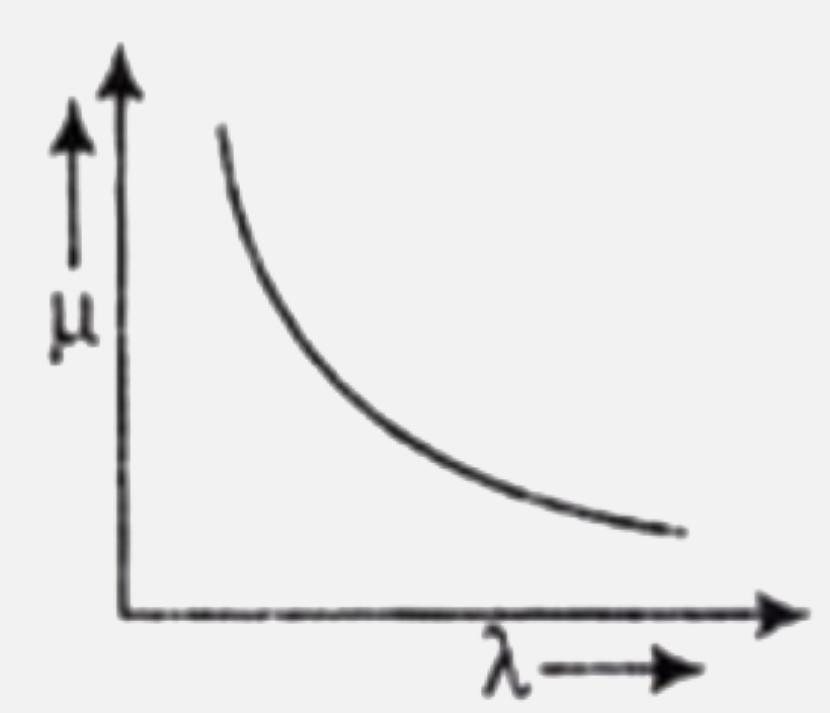
A spectrograph's trihedral prism is manufactured from glass whose refractive index varies with wavelength as n=A+B/λ2, where A and B are constats, with B being equal to 0.010μm2. Making use of the formula from the foregoing problem, find:
(a) how the resolving power of the prism depends on λ, calculate the value of λ/δλ in the vicinity of λ1=434nm and λ2=656nm if the width of the prism's base is b=5.0cm,
(b) the width of the prism's base capacble of resolving the yellow doublet of sodium (589.0 and 589.6nm).View SolutionThe wavelength of green light in air and in glass is 5300 Å and 3533 Å. The refractive index of glass is
View SolutionThe refractive index of glass is 1.5 for light waves of λ=6000 Ã… in vacuum. Its wavelength in glass is
View SolutionThe distance travelled by light in glass (refractive index =1.5) in a nanosecond will be
View SolutionHow does refractive (µ) of a material vary with respect to wavelength (λ)? A and B are constants
View Solution

