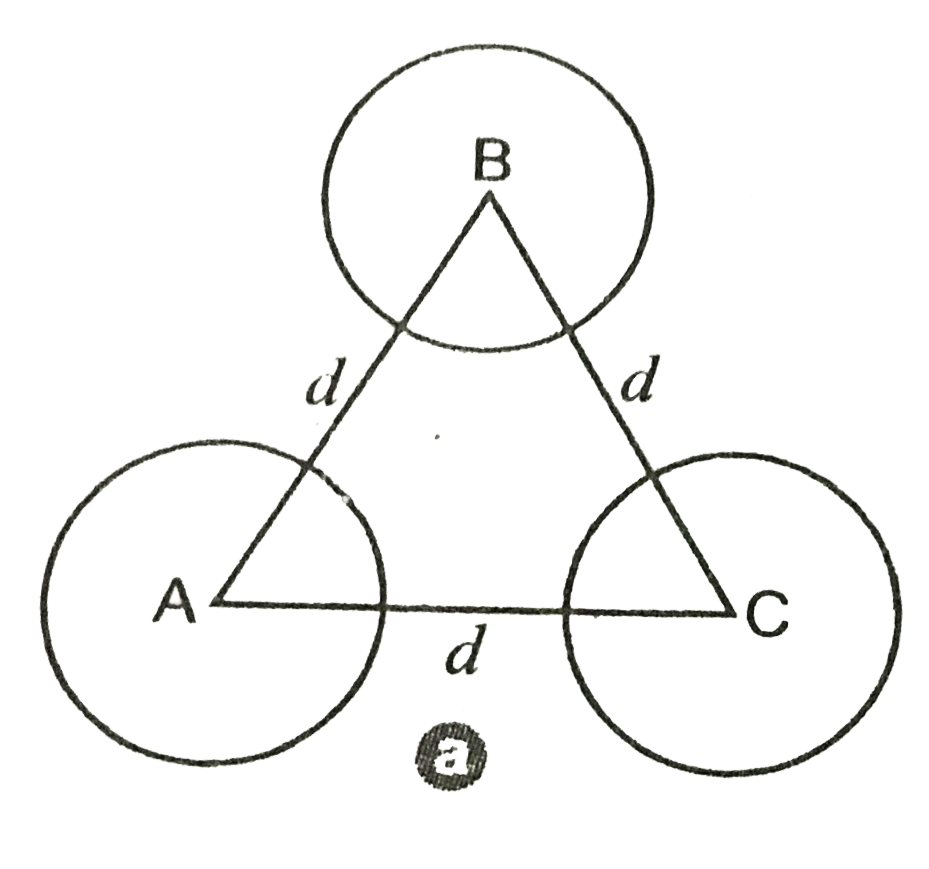
Three uniform spheres, A, B and C each of mass M and radius R are kept in such a way that each sphere touches the other two. What is the magnitude of the gravitational force acting on A due to B and C ?
√3GM24R2
√3GM2R2
3GM24R2
√3GM22R
The correct Answer is:A
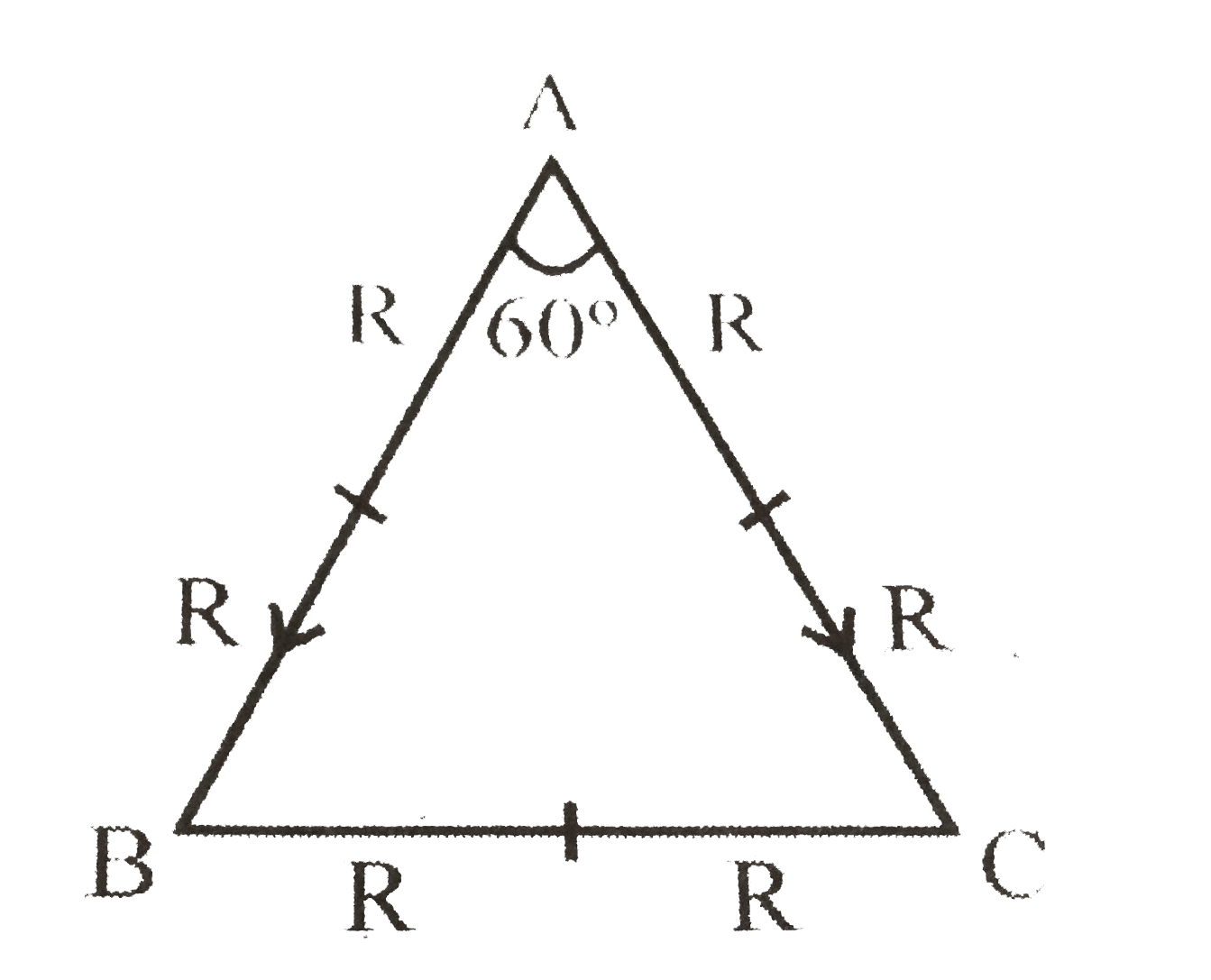
Assume that the mass of each sphere is concentrated at this centre. Then we have a system of three point masses situated at the vertices of an equilateral triangle. This force of attraction on A, due to sphere B is
F1=GM×M(2R)2=GM24R2 along −−→AB and the force on A due to sphere C is F2=GM24R2 along AC. Thus F1=F2 in magnitude, As angule between →F1 and →F2 is 60∘, the magnitude of the resultant force,
F=√F21+F22+2F1F2cos60∘
F=√F21+F21+2F1F1×12=√2F21+F21
∴F=√3F1=√3×GM24R2
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - TEST YOUR GRASP -220videos
GRAVITATION
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - TEST YOUR GRASP20videos
ELECTROSTATICS
- BOOK - MARVEL PUBLICATIONCHAPTER - INTERFERENCE AND DIFFRACTIONEXERCISE - TEST YOUR GRASP20videos
INTERFERENCE AND DIFFRACTION
Similar Questions
Thee uniform spheres each having a mass M and raius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
View SolutionThree uniform spheres, each having a mass M=5kg and radius a=2.5m are kept in such a way that each touches the other two. Find the magnitude of the gravitational force in GN on any of the spheres due to the other two.
View Solution
Knowledge Check
- Question 1 - Select One
Three uniform spheres each of mass m and diameter D are kept in such a way that each touches the other two, then magnitudes of the gravitational force on any one sphere due to the other two is
A3Gm2D2B2√3Gm2D2C√3Gm24D2D√3Gm2D2 - Question 2 - Select One
Three identical spheres, each having a charge q and radius R. are kept in such a way that each touches the other two. The magnitude of the electric force on any sphere due to the other two is
A14πε0(qR)2B√34πε0(qR)2C√316πε0(qR)2D√516πε0(qR)2 - Question 3 - Select One
Two metal spheres each of radius r are kept in contact with each other. If d is the density of the material of the sphere,then the gravitational force between those spheres is proportional to
Ad2r6Bd2r4Cd2r4Dr2d2
Draw circles with centres A,B and C each of radius 3 cm, such that each circle touches the other two circles.
View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is
 View Solution
View SolutionThree solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?
 View Solution
View SolutionThree spheres, each mass M and radius R, are arranged as shown in the figure . The moment of inertia of the system will be
 View Solution
View SolutionInside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
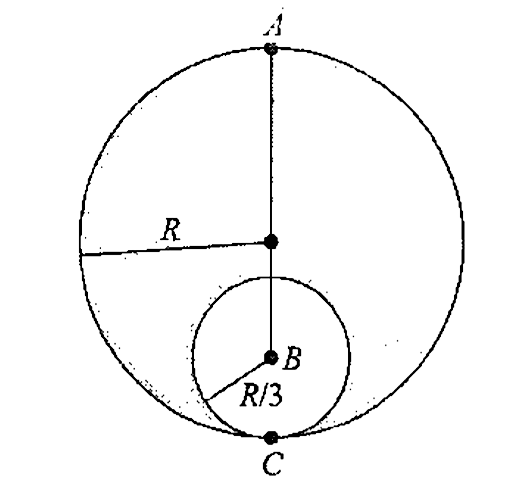 View Solution
View Solution

