A double star is a system of two stars of masses m and 2m, rotating about their centre of mass only under their mutual gravitational attraction. If r is the separation between these two stars then their time period of rotation about their centre of mass will be proportional to
T=2π√L32mG
T?=2π√L33mG
T=2π√L34mG
T=2π√L3mG
The correct Answer is:B
The two starts are at A and B. The system rotates about their centre of mass C. It divides the distence AB = L, in the ratio of 1 : 2.
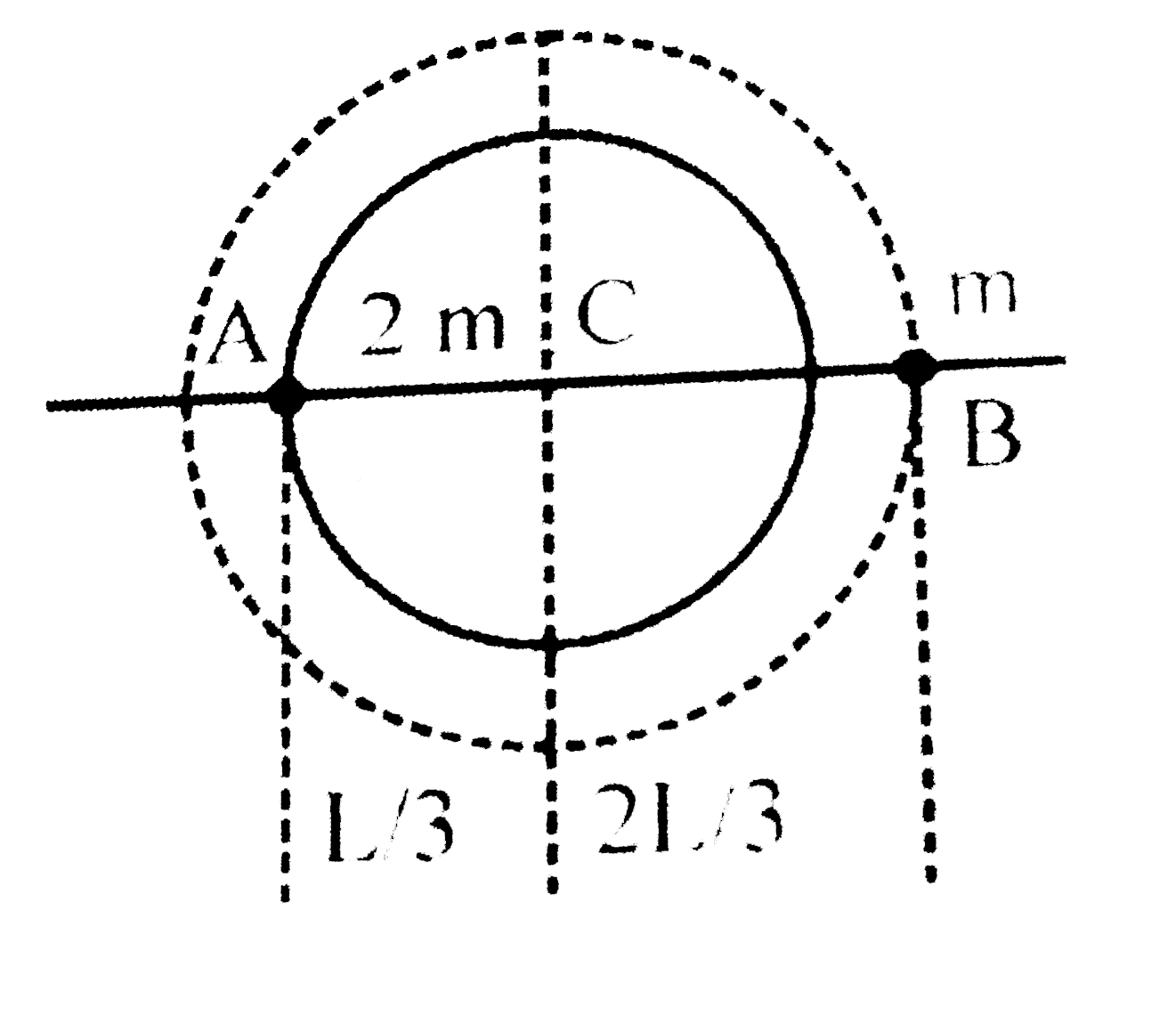
∵2m×L3=m×2L3
Thus AC=L3 and BC=2L3.
The gravitational force of attraction between them is
F=G(2m)(m)L2 and this provides the C.P. force for the mass m' to rotate in a circular of radius 2L3.
∴G.2m2L2=mrω2=m.(2L3)ω2
∵ω2=3GmL3∴(2πT)2=3GmL3
∴T=2π√L33Gm
Topper's Solved these Questions
- GRAVITATION BOOK - MARVEL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - TEST YOUR GRASP -2
20 Videos
- ELECTROSTATICSBOOK - MARVEL PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - TEST YOUR GRASP
20 Videos
- INTERFERENCE AND DIFFRACTIONBOOK - MARVEL PUBLICATIONCHAPTER - INTERFERENCE AND DIFFRACTIONEXERCISE - TEST YOUR GRASP
20 Videos
Similar Questions
A double star is a system of two starts moving around the centre of inertia of the system due to gravitation. Find the distance between the components of the double star, if its total mass equals M and the period of revolution T.
View SolutionIn a double star system, two stars of masses m1 and m2 separated by a distance x rotate about their centre of mass. Find the common angular velocity and Time period of revolution.
View Solution
Knowledge Check
Two particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
Aacceleration of both the particles are equal.Bacceleration of the particle of mass m1 is proportional to m1Cacceleration the particle of mass m1 is proportional to m2.Daccelaration of the particle of mass m1 is inversely proportional to m1.Two particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
Aaccelerations of both the particles are equal.Bacceleration of the particle of mass m1 is proportional to m1.Cacceleration of the particle of mass m1 is proportional to m2.Dacceleration of the particle of mass m1 is inversely proportional to m1.Two stars of masses m and 2m at a distance d rotate about their common centre of mass in free space. The period of revolution is :
A12π√d33GmB2π√d33GmC12π√3Gmd3D2π√3Gmd3
In a double star, two stars one of mass m1 and another of mass m2, with a separation d, rotate about their common centre of mass. Find
(a) an expression for their time period of revolution.
(b) the ratio of their kinetic energies.
(c) the ratio of their angular momenta about the centre of mass.
(d) the total angular momentum of the system.
(e) the kinetic energy of the system.
View SolutionA double star consists of two stars having masses M and 2M. The distance between their centres is equal to r. They revolve under their mutual gravitational interaction. Then, which of the following statements are not correct?
View SolutionTwo stars of masses m1 and m2 distance r apart, revolve about their centre of mass. The period of revolution is :
View SolutionTwo particles of equal mass m go around a circle of radius R under action of their mutual gravitational attraction. The speed of each particle with respect to their centre of mass is
View SolutionIf gravitational attraction between two points masses be given by F=Gm1m2rn. Then the period of a satellite in a circular orbit will be proportional to
View Solution
