The total charge induced in a conducting loop when it is moved in magnetic field depends on
the total change in the magnetic flux
final magnetic flux only
the rate of change of the magnetic flux
initial magnetic flux only
The correct Answer is:A
I=eRandI=dqdt
∴q=∫Idt=∫eRdt=1R∫edt
But e=dϕdt (in magnitude)
∴Q=1R∫dϕdtdt=1R∫dϕ
Thus the total charge induced in the circuit, depends upon R as well as ∫dϕ or the total change in the magnetic flux.
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS EXERCISE - TEST YOUR GRASP - 1630videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS
- BOOK - MARVEL PUBLICATIONCHAPTER - ELASTICITYEXERCISE - Test Your Grasp - 515videos
ELASTICITY
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTRONS AND PHOTONS EXERCISE - TEST YOUR GRASP - 1715videos
ELECTRONS AND PHOTONS
Similar Questions
Current is induced in a conducting loop placed in a magnetic field as shown. Choose correct option.
 View Solution
View SolutionUse Lenz's law to determine the direction of the induced current when a rectangular conducting loop abcd is moved into a region of magnetic field which is directed normal to the plane of the loop away from the reader.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The total charge, induced in a onducting loop when it is moved in magnetic field depend on
Athe rate of change of magnetic fluxBinitial magnetic flux onlyCthe total change in magnetic fluxDfinal magnetic flux only. - Question 2 - Select One
The total charge flown through a conducting loop in a given time duration when it is moved in magnetic field depend on: (
AThe rate of change of magnetic fluxBInitial magnetic flux onlyCThe total change in magnetic fluxDFinal magnetic flux only - Question 3 - Select One
Consider a conducting circular loop placed in a magentic filed as shown. When magnetic field changes with time, magentic flux also changes and emf is induced.
e=−dϕdt
If resistance of loop is R then induced current.
i=eR
For Current, charge must have come into motion. Magnetic force cannot make the statinoary charges to move. Actually there is an induced electric field in the conductor caused by changing magnetic flux, which make the change to move
∫→E.d→l=e=−dϕdt
This induced electric field is non-electrostatic by nature. line integral of →E around a closed path is non-zero

A square non- conducting loop 20 cm on a side is placed in a magnetic field The centre of side AB coincides with the centre of magnetic field The magnetic field is increasing at the rate of 2T/s. Find the magnitude of line integral of induced electric field along path BC.
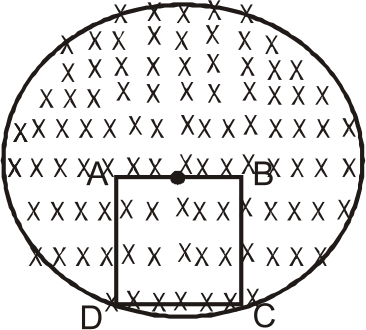 A10 mVB20 mVC30 mVDzero
A10 mVB20 mVC30 mVDzero
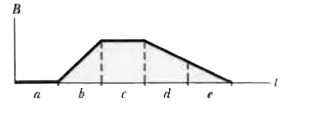
The graph gives the magnitude B(t) of a uniform magnetic field that exists throughout a conducting loop, with the direction of the field perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude of the emf induced in the loop, greatest first.
 View Solution
View SolutionRead the following two statements.
(A) Emf can be induced by changing magnetic field.
(B) Emf must be induced when a conductor is moved inside magnetic field.View SolutionA charge q is moving in a magnetic field then the magnetic force does not depend upon
View Solution
Emf induced in the left arm of the loop, if it is moved out of the magnetic field in 1s with constant speedView SolutionAsseration: The induced emf in a conducting loop of wire will be non zero when it rotates in a uniform magnetic field.
Reason: The emf is induced due to change in magnetic flux.View Solution

