A current I=3sinωt ampere flows through a bulb. The P.D. across the bulb is given by V=4cosωt volt. The power dissipated in the bulb is
12 W
6 W
zero W
3 W
The correct Answer is:C
V=4cos(ωt)=4sin(ωt+π2)
Phase diff. between V and I is π2
∴ Power factor = cos(π)2=0.
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS EXERCISE - TEST YOUR GRASP - 1630videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS
- BOOK - MARVEL PUBLICATIONCHAPTER - ELASTICITYEXERCISE - Test Your Grasp - 515videos
ELASTICITY
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTRONS AND PHOTONS EXERCISE - TEST YOUR GRASP - 1715videos
ELECTRONS AND PHOTONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The potential difference V across and the current I flowing through an instrument in an AC circuit are given by:
V=5cosωt volt
I=2sinωt Amp.AZeroB5 wattC10 wattD2.5 watt - Question 2 - Select One
The potential difference V across and the current I flowing through an instrument in an AC circuit are given by:
V=5cosωt volt
I=2sinωt Amp.AzeroB5 wattC10 wattD2.5 watt - Question 3 - Select One
The potential differences V and the current i flowing through an instrument in an AC circuit of frequency f are given by V=5cosωt and I=2sinωt amperes (where ω=2πf). The power dissipated in the instrument is
AzeroB10WC5WD2.5W
If the current passing through a bulb is 0.2 A and the power of the bulb is 20 W , find the voltage applied across the bulb.
View SolutionAn AC current is given as i=(2cosωt+3sinωt)A.The rms current is "
View SolutionIf the current passing through a bulb is 0.15 A and the power of the bulb is 30 W, find the voltage applied across the bulb.
View SolutionThree 60W,120V light bulbs are connected across a 120V power lines as shown in Fig. 7.26. Find (a) the voltage across each bulb and (b) the total power dissipated in the three bulbs.
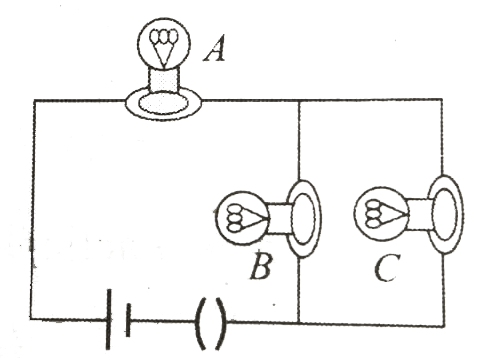 View Solution
View SolutionThe potential difference V and current I flowing through an a.c. circuit are given as V=50cosωt and I=2sinωt, where ω is the angular frequency of a.c. The power dissipated in the circuit is.
View Solution

