A shop keeper sells to two items, colour T.V. sets and DVD players. He can invest Rs. 12,00,000 and can store only 750 items. The cost of color TV and DVD player is Rs. 6500 and Rs. 2800 respectively. He can sell these items at a price of Rs. 8600 and Rs. 3900 respectively. Form the LPP to maximize the profit.
Maximize z=2100x+1100y subject to 6500x+2800y≤1200000,x+y≥750,x≥0,y≥0
Maximize z=2100x+1100y subject to 6500x+2800y≤1200000,x+y≤750,x≥0,y≥0
Maximize z=2100x+1100y subject to 6500x+2800y≥1200000,x+y≤750,x≥0,y≥0
Maximize z=2100x+1100y subject to 6500x+2800y≥1200000,x+y≥750,x≥0,y≥0
The correct Answer is:B
Step by step video, text & image solution for A shop keeper sells to two items, colour T.V. sets and DVD players. He can invest Rs. 12,00,000 and can store only 750 items. The cost of color TV and DVD player is Rs. 6500 and Rs. 2800 respectively. He can sell these items at a price of Rs. 8600 and Rs. 3900 respectively. Form the LPP to maximize the profit. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A dealer deals in two items A and B He has Rs. 15000 to invest and a space to store almost 80 pieces Item A costs him Rs 300 and item B costs him Rs. 150 He can sell items A and B at profits of Rs 40 and Rs 25 respectively Assuming that he can sell all that he buys formulate the above as a linear programming prioblem for maximum profit and solve it graphically
View SolutionA manufacture produces three stationery products Pencil, Eraser and Sharpener which he sells in two markets. Annual sales are indicated below

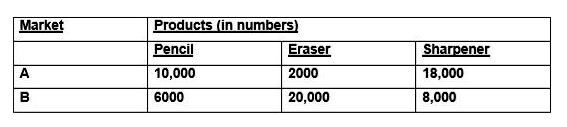
If the unit Sale price of Pencil, Eraser and Sharpener are Rs. 2.50, Rs. 1.50 and Rs. 1.00 respectively, and unit cost of the above three commodities are Rs. 2.00, Rs. 1.00 and Rs. 0.50 respectively, then,
Based on the above information answer the following:
Profit in market A and B respectively are
View Solution
Knowledge Check
A furniture dealer deals in only two items namely tables and chairs. He has Rs. 5000 to invest and space to store at most 60 pieces. A table cost him Rs. 250 and a chair Rs. 60. He can sell a table at a profit of Rs. 15. Assume that he can sell all the items that he produced. The number of constraints in the problem are
A2B3C4D5A dealer wishes to purchase table fans and ceiling fans. He has Rs. 57,600 to invest, and has space to store 40 items. A table fan costs Rs. 750 and ceiling fan costs Rs. 900. He can make profits of Rs. 70 and Rs. 90 by selling a table fan and a ceiling fan respectively. If dealer sell all the fans that he buy, the formulate this problem as LPP, to maximize the profit.
AMaximize z=70x+90y subject to 750x+900y≤57600,x+y≤40,x≥0,y≥0BMaximize z=70x+90y subject to 750x+900y≥57600,x+y≤40,x≥0,y≥0CMaximize z=70x+90y subject to 750x+900y≤57600,x+y≥40,x≥0,y≥0DMaximize z=70x+90y subject to 750x+900y≥57600,x+y≥40,x≥0,y≥0
A manufacture produces three stationery products Pencil, Eraser and Sharpener which he sells in two markets. Annual sales are indicated below

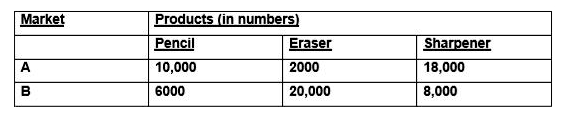
If the unit Sale price of Pencil, Eraser and Sharpener are Rs. 2.50, Rs. 1.50 and Rs. 1.00 respectively, and unit cost of the above three commodities are Rs. 2.00, Rs. 1.00 and Rs. 0.50 respectively, then,
Based on the above information answer the following:
Gross profit in both market
View SolutionA manufacture produces three stationery products Pencil, Eraser and Sharpener which he sells in two markets. Annual sales are indicated below

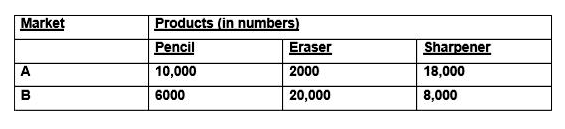
If the unit Sale price of Pencil, Eraser and Sharpener are Rs. 2.50, Rs. 1.50 and Rs. 1.00 respectively, and unit cost of the above three commodities are Rs. 2.00, Rs. 1.00 and Rs. 0.50 respectively, then,
Based on the above information answer the following:
Cost incurred in market A
View SolutionA manufacture produces three stationery products Pencil, Eraser and Sharpener which he sells in two markets. Annual sales are indicated below

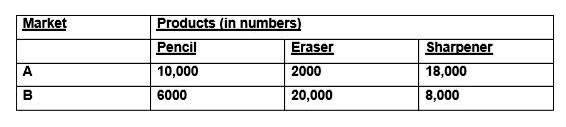
If the unit Sale price of Pencil, Eraser and Sharpener are Rs. 2.50, Rs. 1.50 and Rs. 1.00 respectively, and unit cost of the above three commodities are Rs. 2.00, Rs. 1.00 and Rs. 0.50 respectively, then,
Based on the above information answer the following:
Total revenue of market A
View SolutionA manufacture produces three stationery products Pencil, Eraser and Sharpener which he sells in two markets. Annual sales are indicated below

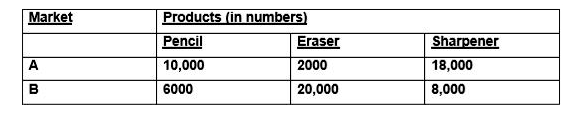
If the unit Sale price of Pencil, Eraser and Sharpener are Rs. 2.50, Rs. 1.50 and Rs. 1.00 respectively, and unit cost of the above three commodities are Rs. 2.00, Rs. 1.00 and Rs. 0.50 respectively, then,
Based on the above information answer the following:
Total revenue of market B
View SolutionA faniture dealer deals in only two itmes - tables and chairs. He has 'Rs. 50000 invest and has storage place of at most 60 pieces. A table costs Rs. 2500 and chair Rs. 500. He estimates that from the sale of one table, he can make a perfect Rs. 250 and that from the sale of one chair a profit of Rs. 75. How many table and chair he should buy from the available money so as to maximise his total profit assuming that he can sell all the items which he buys.
View SolutionIf a shopkeeper sells an item at Rs. 2,700 he makes 8% profit. If he sells the item at Rs. 3,000 what will be the percentage of profit?
View Solution