A particle is moving along X-axis Its acceleration at time t is proportional to its velocity at that time. The differential equation of the motion of the particle is
d2xdt2−kdxdt=0,k>0
d2xdt2+kdxdt=0,k>0
d2xdt2−k=0,k>0
d2xdt2+k=0,k>0
The correct Answer is:A
To solve the problem, we need to derive the differential equation of motion for a particle whose acceleration is proportional to its velocity. Let's go through the steps systematically.
1. Define the Variables:
- Let x(t) be the position of the particle at time t.
- Let v(t)=dxdt be the velocity of the particle.
- Let a(t)=d2xdt2 be the acceleration of the particle.
2. Establish the Relationship:
- According to the problem, the acceleration a is proportional to the velocity v. This can be expressed mathematically as:
a=kv
where k is a positive constant of proportionality (i.e., k>0).
3. Substitute the Definitions:
- Substitute the definitions of acceleration and velocity into the equation:
d2xdt2=kdxdt
4. Rearrange the Equation:
- Rearranging the equation gives us:
d2xdt2−kdxdt=0
5. Final Form of the Differential Equation:
- The resulting differential equation that describes the motion of the particle is:
d2xdt2−kdxdt=0
Conclusion:
Thus, the differential equation of the motion of the particle is:
d2xdt2−kdxdt=0
- Let x(t) be the position of the particle at time t.
- Let v(t)=dxdt be the velocity of the particle.
- Let a(t)=d2xdt2 be the acceleration of the particle.
- According to the problem, the acceleration a is proportional to the velocity v. This can be expressed mathematically as:
a=kv
where k is a positive constant of proportionality (i.e., k>0).
- Substitute the definitions of acceleration and velocity into the equation:
d2xdt2=kdxdt
- Rearranging the equation gives us:
d2xdt2−kdxdt=0
- The resulting differential equation that describes the motion of the particle is:
d2xdt2−kdxdt=0
Thus, the differential equation of the motion of the particle is:
d2xdt2−kdxdt=0
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
For a particle moving along circular path, the radial acceleration ax is proportional to time t. If at is the tangential acceleration, then which of the following will be independent of time t.
AatBar.atCaratDar(at)2 - Question 2 - Select One
A particle moves along x-axis and its acceleration at any time t is a = 2 sin (πt), where t is in seconds and a is in m/s2 . The initial velocity of particle (at time t = 0) is u = 0.
Q. Then the magnitude of displacement (in meters) by the particle from time t = 0 to t = t will be :A2π2sinπt−2tπB−2π2sinπt+2tπC2tπDnone of these - Question 3 - Select One
A particle moves along x-axis and its acceleration at any time t is a = 2 sin (πt), where t is in seconds and a is in m/s2 . The initial velocity of particle (at time t = 0) is u = 0.
Q. Then the distance travelled (in meters) by the particle from time t = 0 to t = t will be :A2π2sinπt−2tπB−2π2sinπt+2tπC2tπDnone of these
A particle is moving along the x-axis and its position-time graph is shown. Determine the sign of acceleration.
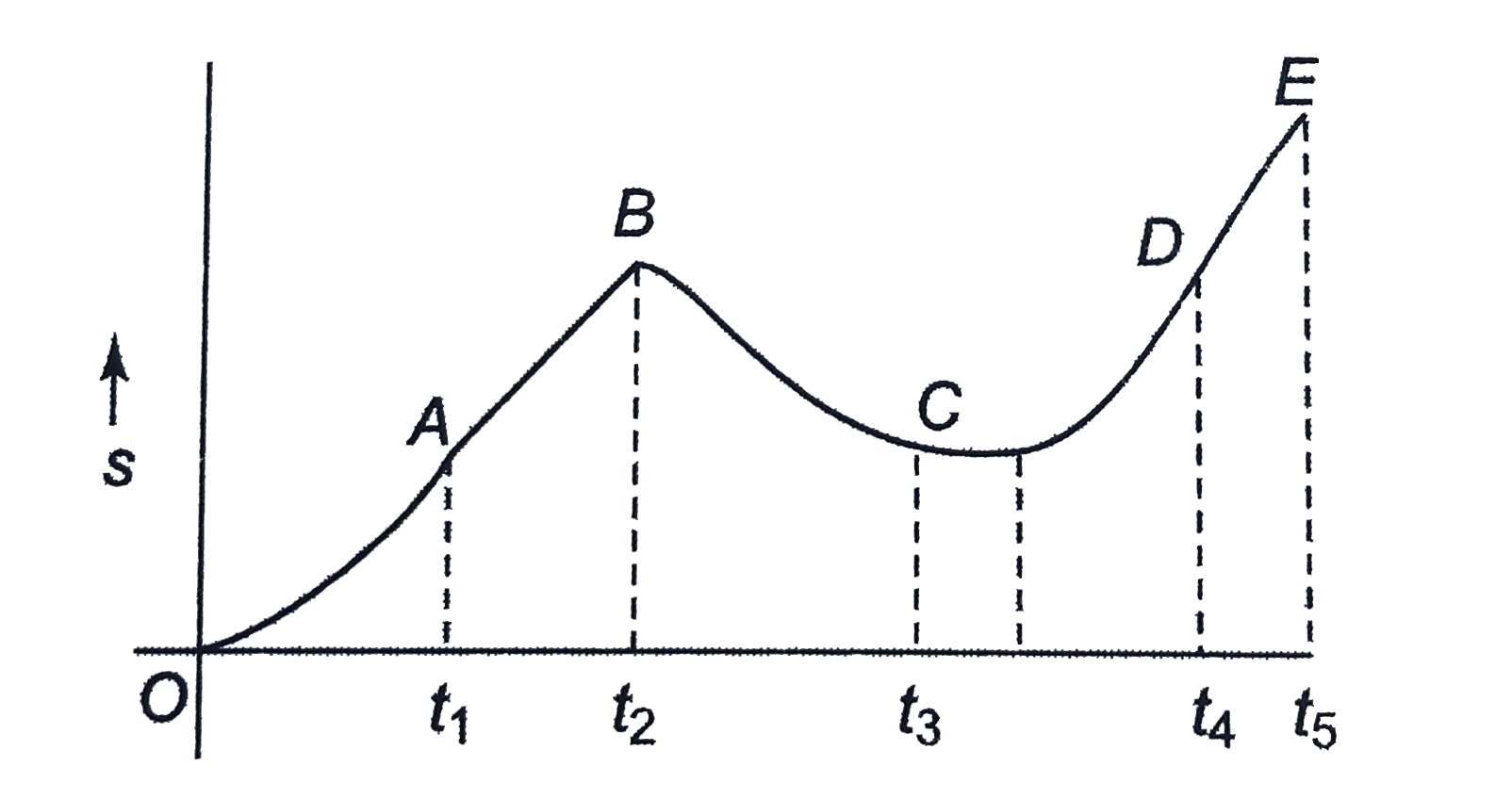 View Solution
View SolutionA particle moves along x-axis and its acceleration at any time t is a = 2 sin (πt), where t is in seconds and a is in m/s2 . The initial velocity of particle (at time t = 0) is u = 0.
Q. Then the distance travelled (in meters) by the particle from time t = 0 to t = 1 s will be :View SolutionA particle is moving under constant acceleration a=kt. The motion starts from rest. The velocity and displacement as a function of time t is
View SolutionIf the distance s covered by a particle in time t is proportional to the cube root of its velocity, then the acceleration is
View SolutionA particle move along y-axis according to equation y+3+4cosωt. The motion of the particle is
View Solution

