80% of all families own a television set. If 10 families are interviewed at random, then the probability that at most three families own a television set is
(8401)(0.8)10
(8401)(0.2)10
(8441)(0.8)10
(8441)(0.2)10
The correct Answer is:D
To solve the problem, we need to find the probability that at most 3 out of 10 families own a television set, given that 80% of families own a TV. This is a binomial probability problem.
1. Identify the parameters of the binomial distribution:
- Let n=10 (the number of families interviewed).
- Let p=0.8 (the probability that a family owns a television).
- Therefore, the probability that a family does not own a television is q=1−p=0.2.
2. Define the event:
- We want to find the probability that at most 3 families own a television set. This can be expressed mathematically as:
P(X≤3)=P(X=0)+P(X=1)+P(X=2)+P(X=3)
where X is the random variable representing the number of families that own a television.
3. Use the binomial probability formula:
The binomial probability formula is given by:
P(X=k)=(nk)pkqn−k
where (nk) is the binomial coefficient.
4. Calculate each probability:
- For k=0:
P(X=0)=(100)(0.8)0(0.2)10=1⋅1⋅(0.2)10=(0.2)10
- For k=1:
P(X=1)=(101)(0.8)1(0.2)9=10⋅0.8⋅(0.2)9=10⋅0.8⋅(0.000000512)=0.000004096
- For k=2:
P(X=2)=(102)(0.8)2(0.2)8=45⋅(0.64)⋅(0.000000256)=0.000007680
- For k=3:
P(X=3)=(103)(0.8)3(0.2)7=120⋅(0.512)⋅(0.0000128)=0.000786432
5. Sum the probabilities:
Now we add the probabilities for k=0,1,2,3:
P(X≤3)=P(X=0)+P(X=1)+P(X=2)+P(X=3)
P(X≤3)=(0.2)10+0.000004096+0.000007680+0.000786432
=0.0000001024+0.000004096+0.000007680+0.000786432
=0.0007983104
6. Final Probability:
Thus, the final probability that at most 3 families own a television set is approximately:
P(X≤3)≈0.000798
- Let n=10 (the number of families interviewed).
- Let p=0.8 (the probability that a family owns a television).
- Therefore, the probability that a family does not own a television is q=1−p=0.2.
- We want to find the probability that at most 3 families own a television set. This can be expressed mathematically as:
P(X≤3)=P(X=0)+P(X=1)+P(X=2)+P(X=3)
where X is the random variable representing the number of families that own a television.
The binomial probability formula is given by:
P(X=k)=(nk)pkqn−k
where (nk) is the binomial coefficient.
- For k=0:
P(X=0)=(100)(0.8)0(0.2)10=1⋅1⋅(0.2)10=(0.2)10
P(X=1)=(101)(0.8)1(0.2)9=10⋅0.8⋅(0.2)9=10⋅0.8⋅(0.000000512)=0.000004096
P(X=2)=(102)(0.8)2(0.2)8=45⋅(0.64)⋅(0.000000256)=0.000007680
P(X=3)=(103)(0.8)3(0.2)7=120⋅(0.512)⋅(0.0000128)=0.000786432
Now we add the probabilities for k=0,1,2,3:
P(X≤3)=P(X=0)+P(X=1)+P(X=2)+P(X=3)
P(X≤3)=(0.2)10+0.000004096+0.000007680+0.000786432
=0.0000001024+0.000004096+0.000007680+0.000786432
=0.0007983104
Thus, the final probability that at most 3 families own a television set is approximately:
P(X≤3)≈0.000798
Topper's Solved these Questions
Similar Questions
Supose that 80 % of all families own a elevision set. If 10 families are interviewed at random, find the probability that seven famileis own a television set .
View SolutionSuppose that 80% of all families own a television set. If 5 families are inervised at random, find the probability that :
(a) three families own a television set.
(b) at least two families own a television set.
View Solution
Knowledge Check
1500 families with 2 children each , were selected randomly and the following data were recorded .

Out of these families , one family is selected at random . What is the probability that the selected family has (i) 2 girls (ii) 1 girl , (iii) no girl ?A0.129 , 0.26 , 0.256B0.068 , 0.45 , 0.482C0.069 , 0.35 , 0.352D0.070 , 0.68 , 0.678
In a colony there are 75 families and each family has two children. Th number of made children of the families is as follows:
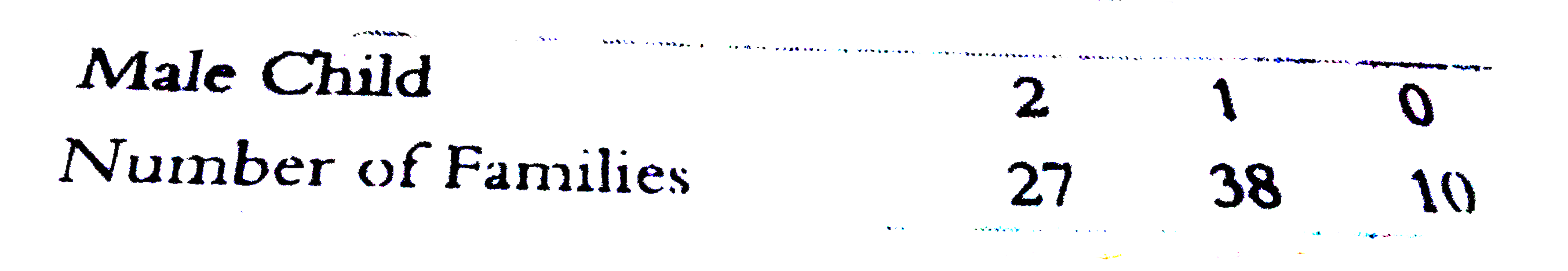
If a family is selected at random, what is the probability that the family has only one male child?
View SolutionThere are two children in a family. Find the probability that at most one boy is there in the family.
View SolutionIn a family of three children, find the probability of having at least two boys.
View SolutionIn a family of three children, find the probability of having at least two boys.
View SolutionIn a locality of 5000 families were chosen at random and the following data was collected

Out of these families, a family is chosen at random. What is the probability that the chosen family has less than 5 but more than 3 members?
View SolutionIn a certain town, 60% of the families own a car, 30% own a house and 20% own both car and house. If a family is randomly chosen, then what is the probability that this family owns a car or a house but not both?
View SolutionA company selected 2300 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a home The information gathered is listed in the table below : if a family is chosen at random, find the probability that the family is: (i) earning Rs.7000-13000 per month and owning exactly 1 vehicle (ii) owning not more than one vehicles. more than 2 vehicles (lii) earning more than Rs. 13000 and owning 2 or (iv) owning no vehicle
View Solution
