A chain of 100 links is 1 m long and has a mass of 2 kg . With the ends fastened together it is set roation at 3000 rpm.then centripetal force on each link is
3.14 N
31.4 N
314 N
3140 N
The correct Answer is:C
To solve the problem of finding the centripetal force on each link of a chain rotating at 3000 rpm, we can follow these steps:
Step 1: Determine the mass of each link
The total mass of the chain is given as 2 kg, and there are 100 links in total. Therefore, the mass of each link can be calculated as:
Mass of each link=Total massNumber of links=2kg100=0.02kg
Step 2: Convert the rotational speed from rpm to radians per second
The angular velocity ω in radians per second can be calculated using the formula:
ω=2πn60
where n is the rotational speed in rpm. Substituting n=3000:
ω=2π×300060=100πrad/s
Step 3: Determine the radius of the circular path
The length of the chain when straight is 1 meter, which becomes the circumference of the circular path when the chain is formed into a circle. The relationship between circumference C and radius r is given by:
C=2πr
Setting C=1m:
1=2πr⟹r=12πm
Step 4: Calculate the centripetal force on each link
The centripetal force Fc acting on each link can be calculated using the formula:
Fc=mω2r
Substituting the values we have:
- m=0.02kg
- ω=100πrad/s
- r=12πm
Now substituting these into the centripetal force formula:
Fc=0.02×(100π)2×12π
Calculating (100π)2:
(100π)2=10000π2
Now substituting this back into the equation for Fc:
Fc=0.02×10000π2×12π
Simplifying:
Fc=0.02×10000×π22π=0.02×10000×π2=100πN
Step 5: Calculate the numerical value of the centripetal force
Using π≈3.14:
Fc≈100×3.14=314N
Final Answer
The centripetal force on each link is approximately 314 N.
---
The total mass of the chain is given as 2 kg, and there are 100 links in total. Therefore, the mass of each link can be calculated as:
The angular velocity ω in radians per second can be calculated using the formula:
The length of the chain when straight is 1 meter, which becomes the circumference of the circular path when the chain is formed into a circle. The relationship between circumference C and radius r is given by:
The centripetal force Fc acting on each link can be calculated using the formula:
- ω=100πrad/s
- r=12πm
Using π≈3.14:
The centripetal force on each link is approximately 314 N.
Topper's Solved these Questions
Similar Questions
A body weighing 13 kg is suspended by two strings 5 m and 12 m long, their other ends being fastened to the extremities of a rod 13 m long. If the rod be so held that the body hangs immediately below the middle point. The tensions in the strings are (1) 12 kg and 13 kg (2) 5 kg and 5 kg (3) 5 kg and 12 kg (4) 5 kg and 13 kg
View SolutionIf Fig. 5-48, a chain consisting of five links, each of mass 0.100 kg, is lifted vertically with constant acceleration of magnitude a=2.50 m/s2. Find the magnitudes of (a) the force on link 1 from link 2, (b) the force on link 2 from link 3, (c) the force on link 3 from link 4, and (d) the force on link 4 from link 5. Then find the magnitudes of (e) the force →F on the top link from the person lifting the chain and (f) the net force accelerating each link.
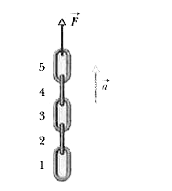 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A chain of 125 links is 1.25 m long and has a mass of 2 kg with the ends fastened together it is set rotating at 3000 revmin. Find the centripetal force on each link -
A3.14 NB314 NC13.14ND1314N - Question 2 - Select One
A chain of 125 links is 1.25 m long and has mass of 2 kg with the ends fastened together. It is set for rotating at 50 revolutions per second. The centripetal force on each link is
A3.14 NB0.314 NC314 NDNone of these - Question 3 - Select One
A store of mass 1 kg , attached at the end of a 1 m long string is whirled in a horizontal circle . IF the string makes an angle of 30∘ with the vertical , then the approximate value of the centripetal force acting on the stone is (g=10m/s2)
A4NB5NC6ND7N
A particle of mass 2 kg is moving along a circular path of radius 1 m. If its angular speed is 2π rad s−1, the centripetal force on it is
View SolutionA chain of 5 links each of mass 0.1 kg is lifted vertically with a constant acceleration 1.2 ms2. The force of interaction between the top link and the one immediately below it is
View SolutionA body of mass 5 kg is moving in a circle of radius m 1 with an angular velocity of 2 radian/sec . The centripetal force is
View SolutionA ring of mass 100 kg and diameter 2 m is rotating at the rate of (300π) rpm. Then
View SolutionIf a body of 5 kg is moving in a circle of radius 5 m with a velocity 100 m s−1, then the centripetal force acting on the body is
View Solution

