In a well of death, motor cycle rides round the inner wall of a hollow cylindrical chamber. If the radius of the cylindrical chamber is 8 m . What would be minimum speed of the rider to prevent him from sliding down? (g=10m/s2,μ=0.2)
10m/s
20m/s
30m/s
40m/s
The correct Answer is:B
v=√rgμ=8×1002=√400=20m/s
Topper's Solved these Questions
Similar Questions
A buket full of water is revolved in a vertical circle of radius 1m . What is the minimum frequency of revolution , required to prevent the water from failing down ? [g=10m/s2]
View SolutionIn the motorcycle cylindrical surface of 18 m diameter. What should be the minimum speed of the motorcyclist to prevent him from sliding down? The coefficient of friction is μ<<0.8. Take the motorcycle to be a point mass.
View Solution
Knowledge Check
In a cylindrical well of death , a motor cyclist rides around the inner wall in horizontal circles. If the diameter of well of death is 18 m , then the minimum speed of cyclist , so as to prevent him from sliding down will be (μ=0.8andg=10m/s2)
A1.06m/sB10.6km/sC0.106m/sD10.6m/sIn a 'well of death' a ride drives round the inner wall of a hollow cylindrical chamber of siameter 20 m .If the coefficient of force friction between tyres and inner wall of a hollow cylinder is 0.5, then the minimum speed of the rider without sliding down will be
A7m/sB14m/sC2√7m/sD7√2m/sA motorcyclist rides in a horizontal circle along the inner wall of cylindrical chamber of radius r. If the coefficient of friction between the tyres and the wall of is μ, the minimum angular speed to prevent him from sidding down is
A√rμgB1r√μgC√grμD√rμg
In the motorcycle stunt called " the well of death" the track is vertical cylindrical surface of 18 m radius.take the motorcyle to be a point mass and μ=0.8. The minimum angular speed of the motorcycle to prevent him from sliding down should be
View SolutionA motor cycle rides in a hollow sphere in a verticle circle of radius 30 m .What will be the minimum speed required so that he does not lose contact with the surface of sphere at the highest point?
View SolutionA motor cyclist rides along a horizontal circle on the certicle cylindrical wall of a metal cylinder the radius of the cylinder is 10 m .If the speed is 20m/s and accele ration due to gravity is 10m/s2 then the least value of the coefficient of friction will be ,
View SolutionWater is filled in a cylindrical container to a height of 3m. The ratio of the cross-sectional area of the orifice and the beaker is 0.1. The square of the speed of the liquid coming out from the orifice is (g=10m/s2).
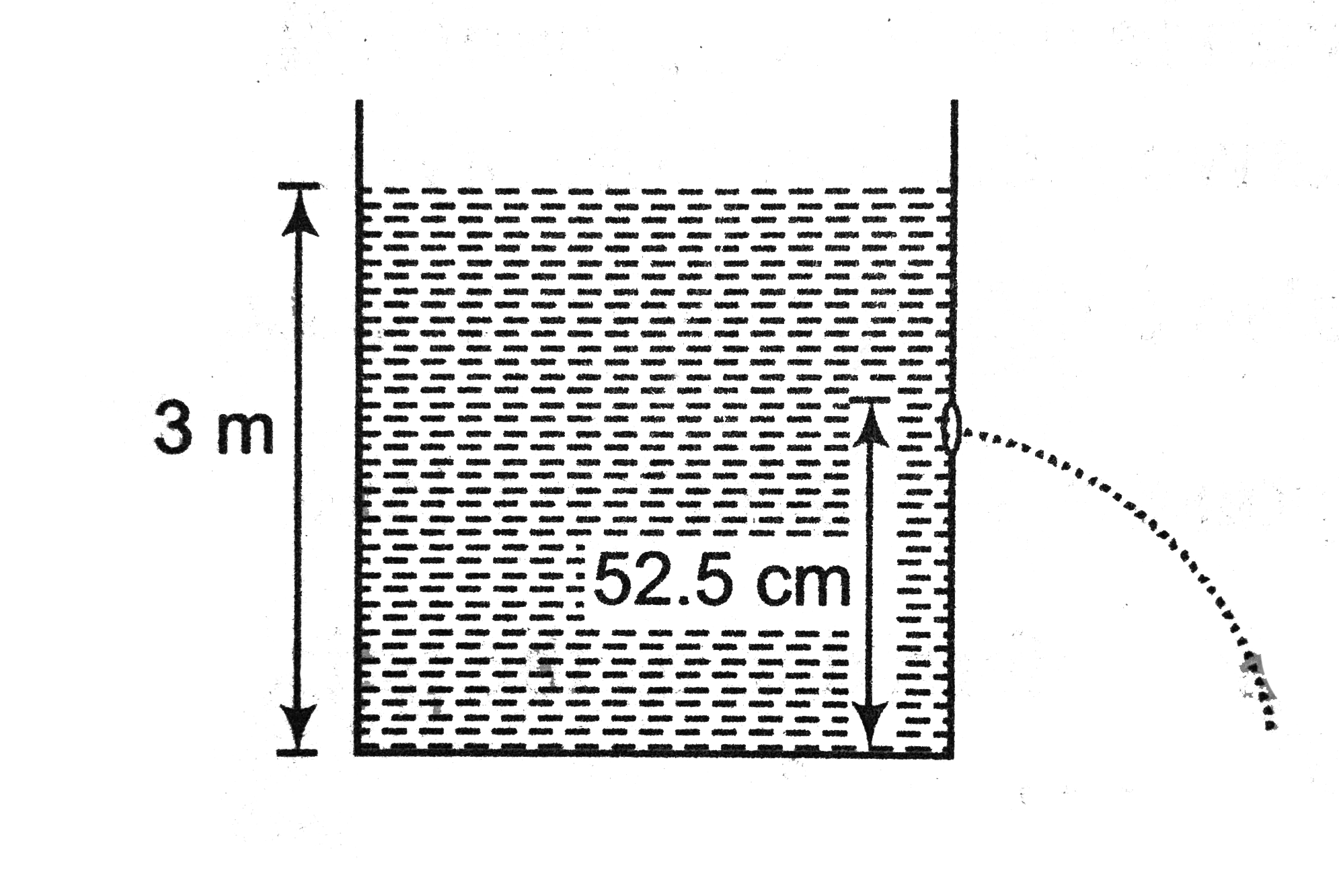
View SolutionThe 'well of death' in a circus consists of a vertical hollow cylinder of radius 9 m A motor cyclist rides on its wall with sufficient speed to prevent him from sliding down . If coefficient of friction is 0.9, the minimum speed the motor cyclist should he is
(g=10ms−2)
View Solution
