Two identical particles A and B are situated respectively at the midpoint and at the end of a string. The particles always remain collinear and move in concentric circles. The ratio of the tensions
T1andT2 will be
1:1
1:3
2:3
3:2
The correct Answer is:B
N=n1+n22×t=4+02
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the arrangement in fig is given a downward acceleration then the ratio of tensions T1 and T2 is strings is-
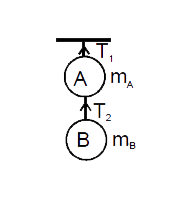 A(mA+mB)/mBB(mA+mB)/mACmA−mBmA+mBDNone of these
A(mA+mB)/mBB(mA+mB)/mACmA−mBmA+mBDNone of theseA particle of mass m1 is fastened to one end of a massless string and another particle of mass m2 is fastened to the middle point of the same string. The other end of the string being fastened to a fixed point on a smooth horizontal table. The particles are then projected, so that the two particles and the string are always in the same straight line and describe horizontal circles. Then, the ratio of rotations in the two parts of the string is :
Am1/(m1+m2)B(m1+m2)/m1C(2m1+m2)/2m1D2m1/(m1+m2)A particle of mass m1 is fastened to one end of a string and one of m2 to the middle point, the other end of the string being fastened to a fixed point on a smooth horizontal table The particles are then projected, so that the two portions of the string are always in the same straight line and describes horizontal circles find the ratio of tensions in the two parts of the string
 Am1m1+m2Bm1+m2m1C2m1+m22m1D2m1m1+m2
Am1m1+m2Bm1+m2m1C2m1+m22m1D2m1m1+m2
Determine the tensions T1 and T2 in the string as shown in figure.
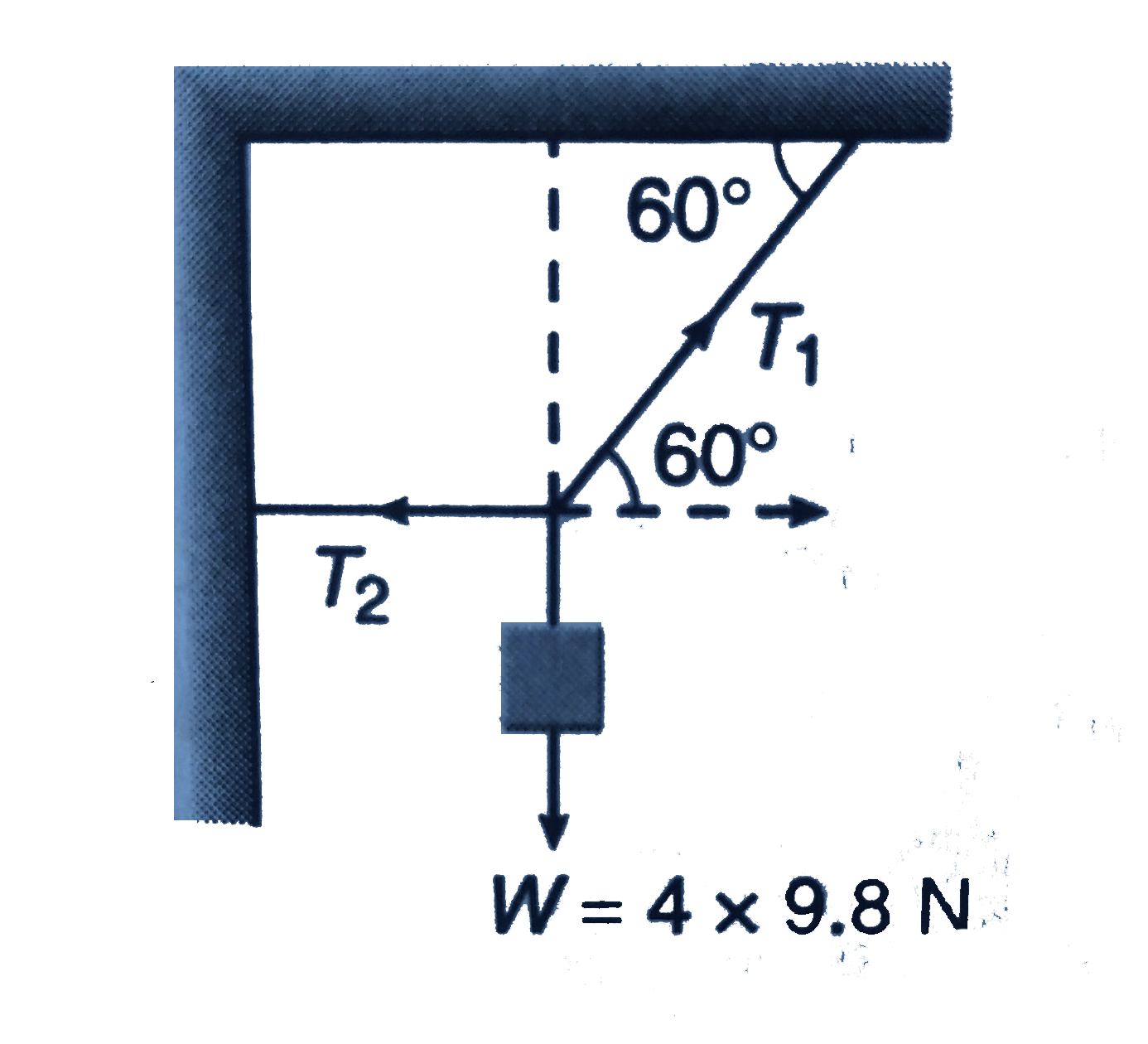
View SolutionThree identical particles are joined together by a thread as shown in figure. All the three particles are moving in a horizontal plane. If the velocity of the outermost particle is v0, then the ratio of tensions in the three sections of the string is (TBC:TAB:TDA)

View SolutionTwo particles are moving in different circles in same plane with different angular velocities as shown in figure. At t = 0, initial positions of particles A and B are shown by dots on the respective circles. Initial distance between particles is 1m. Particle A move anticlockwise in the first circle whereas B moves clockwise in the second circle. Angle described (rotated) by A and B in time 't' are θA=(π2t) and θB=(πt) respectively. here θ is in radian and t is in second. Radius of each circle is shown in diagram.
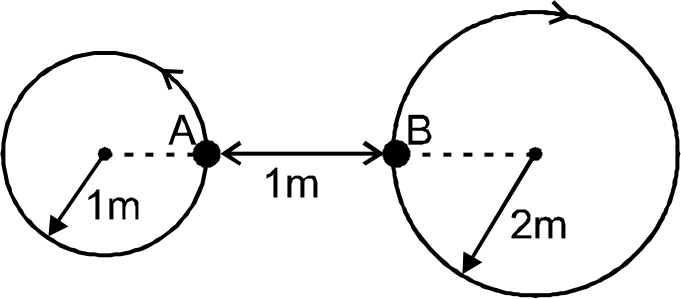
At time t=1 sec. the magnitude of acceleration of A with respect to B is
View SolutionTwo particles are moving in different circles in same plane with different angular velocities as shown in figure. At t = 0, initial positions of particles A and B are shown by dots on the respective circles. Initial distance between particles is 1m. Particle A move anticlockwise in the first circle whereas B moves clockwise in the second circle. Angle described (rotated) by A and B in time 't' are θA=(π2t) and θB=(πt) respectively. here θ is in radian and t is in second. Radius of each circle is shown in diagram.
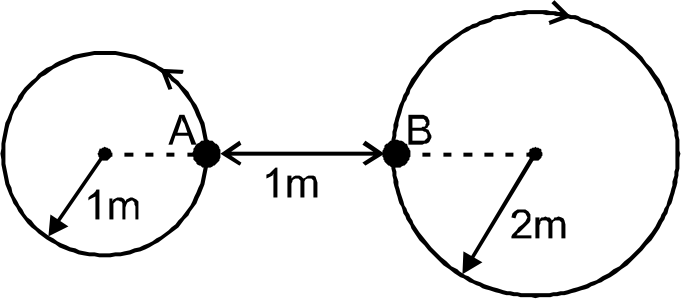
Find the magnitude of acceleration of A at t=1 sec
View SolutionThree identical particles are joined together by a thread as shown in figure All the partical are moving in a horizontal plane If the vertical of the outermost particle is v0 then the ratio of tension in the three sections of the string (T1:T2:T3=?) is
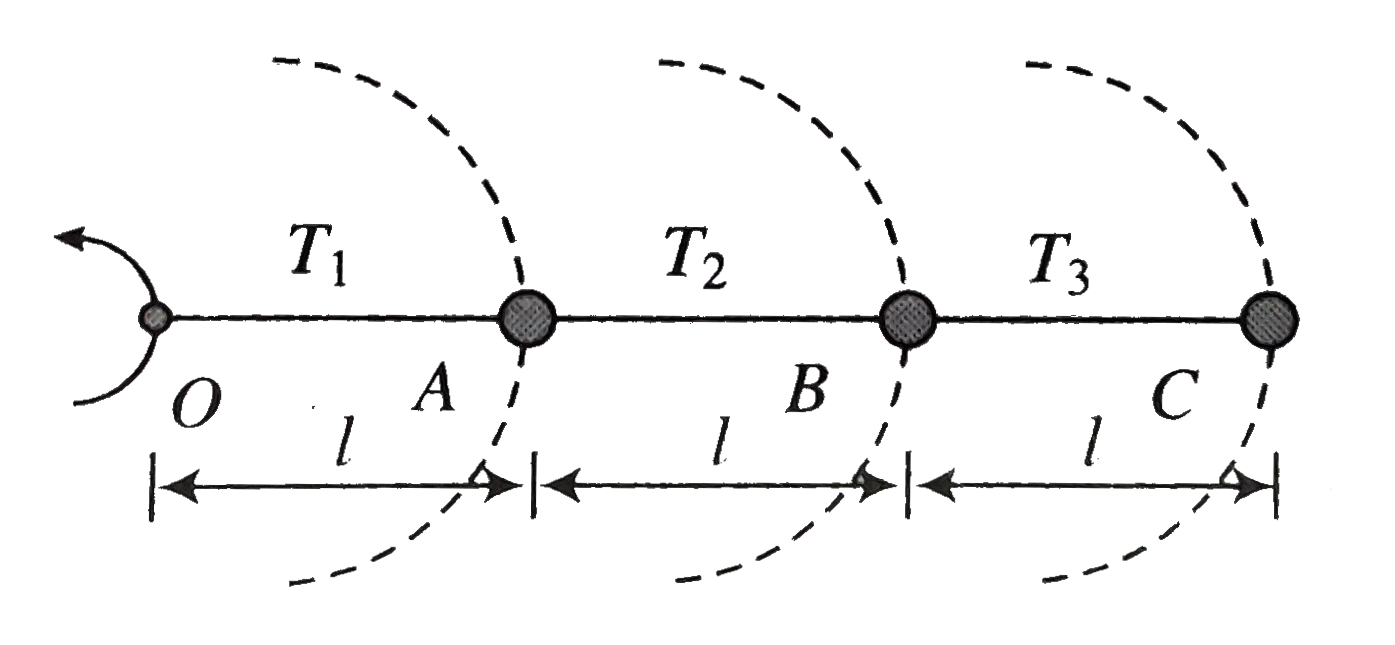
View Solution


