Two point charges +9e and +e are kept at a distance 'a' from each other. A third charge is placed at a distance 'x' from +9e on the line joining the above two charges. For the third charge to be in equilibrium 'x' is
The correct Answer is:A
To solve this problem, we need to find the position x where a third charge −q should be placed such that it is in equilibrium due to the forces exerted by the charges +9e and +e.
1. Identify the Forces Acting on the Third Charge:
- The third charge −q will experience an attractive force towards +9e and a repulsive force from +e.
2. Assume the Position of the Third Charge:
- Let the third charge −q be placed at a distance x from the charge +9e. Therefore, the distance from +e will be a−x.
3. Write the Force Equations:
- The force due to +9e on −q:
F1=k9e⋅qx2
- The force due to +e on −q:
F2=ke⋅q(a−x)2
4. Set the Forces Equal for Equilibrium:
- For the third charge to be in equilibrium, the magnitudes of these forces must be equal:
k9e⋅qx2=ke⋅q(a−x)2
5. Simplify the Equation:
- Cancel out the common terms k and q:
9ex2=e(a−x)2
- Simplify further:
9x2=1(a−x)2
6. Solve for x:
- Cross-multiply to solve for x:
9(a−x)2=x2
- Expand and simplify:
9(a2−2ax+x2)=x2
9a2−18ax+9x2=x2
9a2−18ax+8x2=0
7. Solve the Quadratic Equation:
- This is a quadratic equation in x:
8x2−18ax+9a2=0
- Use the quadratic formula x=−b±√b2−4ac2a:
x=18a±√(18a)2−4⋅8⋅9a22⋅8
x=18a±√324a2−288a216
x=18a±√36a216
x=18a±6a16
- This gives two solutions:
x=24a16=3a2
x=12a16=3a4
8. Select the Valid Solution:
- Since x must be less than a (as it is the distance from +9e), the valid solution is:
x=3a4
Final Answer:
The distance x from the charge +9e where the third charge −q should be placed to be in equilibrium is 3a4.
- The third charge −q will experience an attractive force towards +9e and a repulsive force from +e.
- Let the third charge −q be placed at a distance x from the charge +9e. Therefore, the distance from +e will be a−x.
- The force due to +9e on −q:
F1=k9e⋅qx2
- The force due to +e on −q:
F2=ke⋅q(a−x)2
- For the third charge to be in equilibrium, the magnitudes of these forces must be equal:
k9e⋅qx2=ke⋅q(a−x)2
- Cancel out the common terms k and q:
9ex2=e(a−x)2
- Simplify further:
9x2=1(a−x)2
- Cross-multiply to solve for x:
9(a−x)2=x2
- Expand and simplify:
9(a2−2ax+x2)=x2
9a2−18ax+9x2=x2
9a2−18ax+8x2=0
- This is a quadratic equation in x:
8x2−18ax+9a2=0
- Use the quadratic formula x=−b±√b2−4ac2a:
x=18a±√(18a)2−4⋅8⋅9a22⋅8
x=18a±√324a2−288a216
x=18a±√36a216
x=18a±6a16
- This gives two solutions:
x=24a16=3a2
x=12a16=3a4
- Since x must be less than a (as it is the distance from +9e), the valid solution is:
x=3a4
The distance x from the charge +9e where the third charge −q should be placed to be in equilibrium is 3a4.
Topper's Solved these Questions
Similar Questions
Two idential point charges Q are kept at a distance r from each other. A third point charge is placed on the line joing the above two charges such that all the three charges are in equilibrium. The third charge
(a) should be of magnitude q=………..
(b) should be of sign .......
(c ) should be placed ........ .View SolutionTwo equal charges, +Q each, are at a distance r from each other. A third charge is placed on the line joining the above two charges such that all these charges are in equilibrium. Find q, in terms of Q.
View Solution
Knowledge Check
- Question 1 - Select One
A charge q is placed at the centre of the line joining two equal charges Q. The system of the three charges will be in equilibrium , if q is equal to
A−Q2B−Q4C+Q4D+Q2 - Question 2 - Select One
A charge q is placed at the centre of the line joining two equal charges Q. The system of the three charges will be in equilibrium if q is equal to:
A(a) −Q2B(b) −Q4C(c) +Q4D(d) +Q2 - Question 3 - Select One
Two point charges +q and −q are placed a distance x apart. A third charge is so placed that al the three charges are in equilibrium. Then
Auknknown charge is −4q/9Bunknown charge is −9q/4Cit should be at (x/3)from smaller chargge between themDnone of these
A charge q is placed at the centre of the line joining two equal charges Q. Show that the system of three charges will be in equilibrium if q=−Q4.
View SolutionTwo point charges +5μCand−2μC are kept at a distance of 1m in free space. The distance between the two zero potential points on the line joining the charges is
View SolutionTwo point charges +4q and +q are placed at a distance L apart. A third charge Q is so placed that all the three charges are in equilibrium. Then location. And magnitude of the third charge will be
View SolutionTwo positively charged particles each having charge Q and are d distance apart. A third charge is introduced in midway on the line joining the two charges. Find the nature and magnitude of third charge so that the system is in equilibrium.
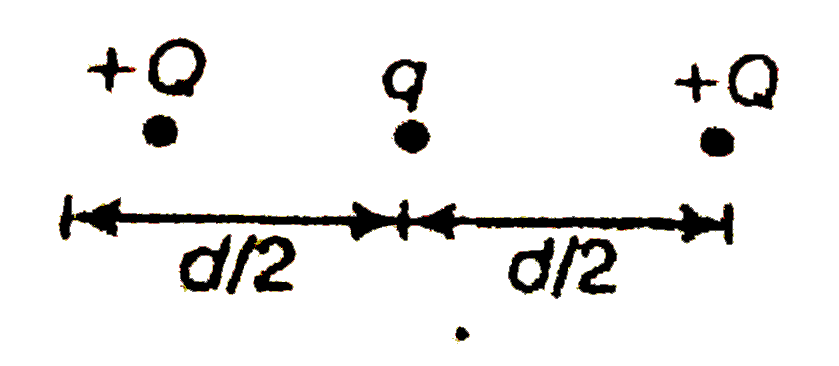 View Solution
View SolutionA charge q is placed at the centre of the line joining two equal charges Q. The system of the three charges will be in equilibrium if q is equal to:
View Solution

