A conductor of length of l and area of cross section A has n number of electrons per unit volume of the conductor. The total charge carried by the conductor is
nA/e
enAl
nAle
n⋅e
The correct Answer is:A
To find the total charge carried by a conductor of length L and cross-sectional area A with n number of electrons per unit volume, we can follow these steps:
1. Determine the Volume of the Conductor:
The volume V of the conductor can be calculated using the formula:
V=A×L
where A is the area of cross-section and L is the length of the conductor.
2. Calculate the Total Number of Electrons:
The total number of electrons Ntotal in the conductor can be found by multiplying the number of electrons per unit volume n by the volume V:
Ntotal=n×V=n×(A×L)
3. Charge of a Single Electron:
The charge of a single electron e is approximately 1.6×10−19 coulombs.
4. Calculate the Total Charge:
The total charge Q carried by the conductor can be calculated by multiplying the total number of electrons Ntotal by the charge of a single electron e:
Q=Ntotal×e=(n×A×L)×e
5. Final Expression for Total Charge:
Therefore, the total charge Q carried by the conductor is given by:
Q=n×A×L×e
Final Answer:
The total charge carried by the conductor is:
Q=n×A×L×e
The volume V of the conductor can be calculated using the formula:
V=A×L
where A is the area of cross-section and L is the length of the conductor.
The total number of electrons Ntotal in the conductor can be found by multiplying the number of electrons per unit volume n by the volume V:
Ntotal=n×V=n×(A×L)
The charge of a single electron e is approximately 1.6×10−19 coulombs.
The total charge Q carried by the conductor can be calculated by multiplying the total number of electrons Ntotal by the charge of a single electron e:
Q=Ntotal×e=(n×A×L)×e
Therefore, the total charge Q carried by the conductor is given by:
Q=n×A×L×e
The total charge carried by the conductor is:
Q=n×A×L×e
Topper's Solved these Questions
- BOOK - NIKITA PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Multiple Choice Questions314videos
CURRENT ELECTRICITY
- BOOK - NIKITA PUBLICATIONCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Multiple Choice Questions (Examples for Practice)8videos
COMMUNICATION SYSTEMS
- BOOK - NIKITA PUBLICATIONCHAPTER - ELASTICITYEXERCISE - MCQ314videos
ELASTICITY
Similar Questions
There is a conducting wire of length l and radius of cross section r. The number of free electrons per unit volume of the conductor is n and the mobility of electrons is μ. A battery of potential difference V is connected across its length. Find electric current flowing through the wire. Assume e as the magnitude of charge on electron.
View SolutionIs current density a vector or a scalar quantity ? Deduce the relation between current density and potential difference across a current carrying conductor of length l, area of cross-section A, and number density of free electrons n. How does the current density, in a conductor vary with (a) increases in potential gradient ? (b) increase in temperature? ( c) increase in length? (d) increase in area of cross-section? (Assume that the other factors remain constant in each case).
View Solution
Knowledge Check
- Question 1 - Select One
A conductor of length l and area of cross-section A has n number of electrons per unit volume of the conductor. The current flowing through conductor in time t is given by
AI=nAletBI=nAlCI=enAltDI=net - Question 2 - Select One
A conductor of length l and area of cross-section A has a resistance R then its specific resistance is
Aρ=RAlBρ=RAlCρ=lRADρ=R2Al - Question 3 - Select One
In a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor. A uniform wire of length 2.0 m and cross-sectional area 10−7m2 carries a current of 1.6 A. If there are 1028 free electrons per m in copper, the drift speed of electrons in copper is
A2mm/sB5mm/sC10mm/sD1m/s
A current I is passed through a silver strip of width d and area of cross-section A. The number of free electrons per unit volume is n
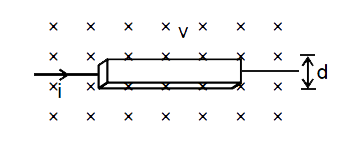
Due to the magnetic force, the free electrons get accumulated on one side of the conductor along its length. This produces a transverse electric field in the conductor which opposes the magnetic force on the electrons. Find the magnitude of the electric field which will stop further accumulation of electrons.View SolutionIn a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor. A constant potential difference is maintained between the ends of a conductor having nonuniform cross-section. Which of the following quantities will not change along the length of the conductor
View SolutionIf A is the area of cross section of conductor, vd is the drift velocity of electrons and n is the number of electrons per unit volume, then current density through conductor is
View SolutionA cylindrical conductor of length .l. and uniform area of cross section .A. has resistance .R.. The area of cross section of another conductor of same material and same resistance but of length .2l. is
View SolutionNet charge in a current-carrying conductor is
View Solution

