Two cells of 1.5 V and 2 V , having internal resistances of 1Ω and 2Ω respectively, are connected in parallel so as to read the current in the same direction through an external resistance of 5Ω . The current in the external resistance will be
517A
175A
512A
125A
The correct Answer is:A
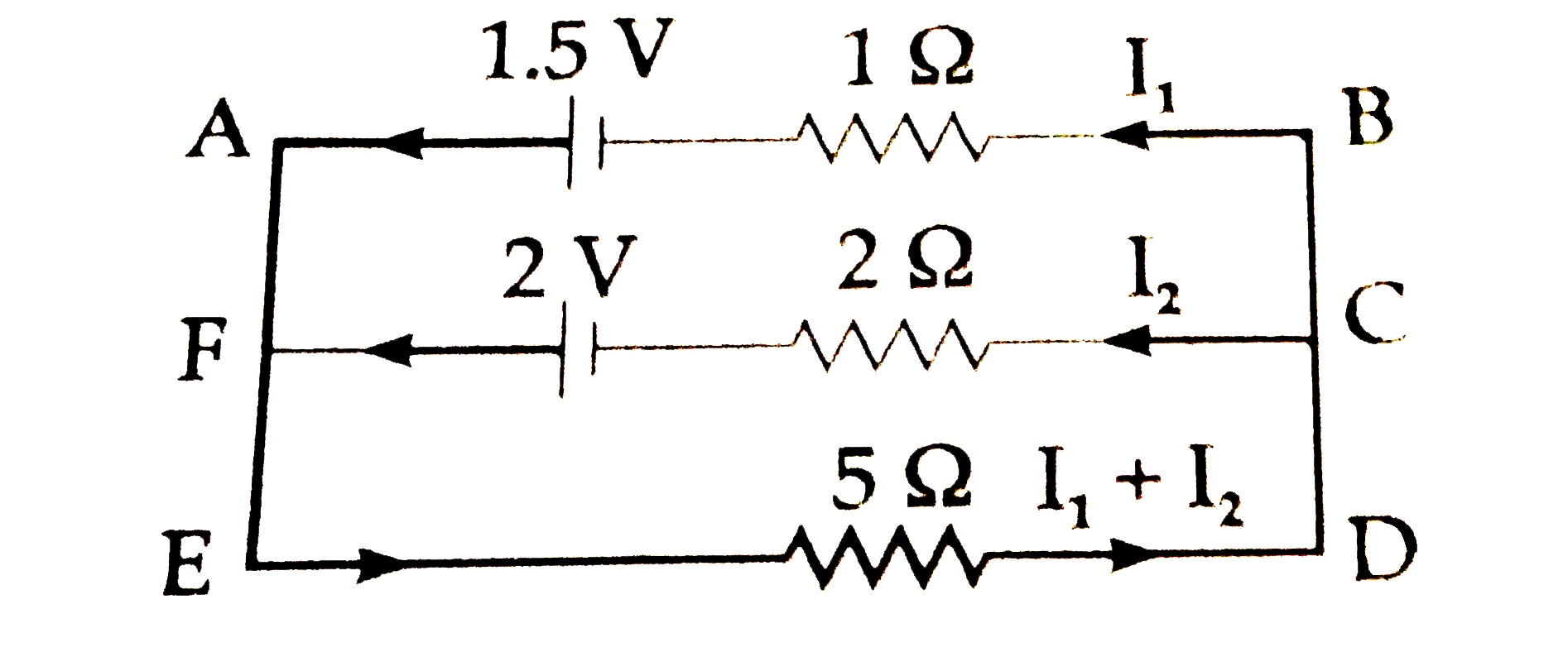
Applying K.V.L. for the loop ABCFA,
we have, −1.5+I1−2I2+2=0
I1−2I2=−0.5 ...(i)
By appling K.V.L. for the loop FCDEF,
we have, −2+2I2+5(I1+I2)=0
5I1+7I2=2 .....(ii)
To solve equation (i) and (ii), multiply equation (i) by (7) and equation (ii) by (2), we have,
7I1−14I2=−3.510I1+14I2=4¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ 17I1=0.5
∴I1=0.517=134A
By substituting value of I1 in equation (ii), we have,
I2=934A
∴ Current through external resistance is,
I1+I2=134+934=1034=517A
Topper's Solved these Questions
- BOOK - NIKITA PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Multiple Choice Questions314videos
CURRENT ELECTRICITY
- BOOK - NIKITA PUBLICATIONCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Multiple Choice Questions (Examples for Practice)8videos
COMMUNICATION SYSTEMS
- BOOK - NIKITA PUBLICATIONCHAPTER - ELASTICITYEXERCISE - MCQ314videos
ELASTICITY
Similar Questions
Two cells of 1.5 V and 2 V , having internal resistances of 1Ω and 2Ω respectively, are connected in parallel so as to read the current in the same direction through an external resistance of 5Ω . The current in the external resistance will be
View SolutionTwo cells of emf 1.5 V and 2 V and internal resistance 1Ω and 2Ω respectively are connected in parallel to pass a current in the same direction through an external resistance of 5Ω.
(i) Draw the circuit diagram.
(ii) Using Kirchhoff's laws, calculate the current through each branch of the circuit and potential difference across the 5Ω resistor.View Solution
Knowledge Check
- Question 1 - Select One
Two cells of e.m.f. 2.5 V and 2.0 V having internal resistance of 1Ω and 2Ω respectively are connected in parallel with similar poles connected together so as to send the current in the same direction through an external resistance of 2Ω. The current in the external resistance is
A0.87 AB1.29 AC1.00 AD2.29 A - Question 2 - Select One
Two batteries of emfs 2 V and 1 V of internal resistances 1Ωand2Ω respectively are connected in parallel. The effective emf of the combination is
A32VB53VC35VD2V - Question 3 - Select One
Four cell each of emf 2 V and internal resistance 1 ohm are connected n parallel with an external resistance of 6 ohm. The current in the external resistance is
A0.32 AB0.16 AC0.2 AD0.6 A
Two cells of emfs 1.5 V and 2.0 V having internal resistances 0.2Ω and 0.3Ω respectively are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.
View SolutionTwo cells of emfs 1.5 V and 2.0V internall resistance 1Ω and 2Ω are connected in parallel so as to send current in the same direction through an external resistance of 5Ω.
(i) Draw the circuit diagram. (ii) Using Kirchhoff's rules, calculate.
(a) current through each branch of the circuit (b) potential difference across the 5Ω resistance.View SolutionTwo cells of emfs 1.5 V and 2.0v having internal resistance 0.2Σ and 0.3 Σ respectively are connected in parallel . Calculate the emf and internal resistance of the equivalent cell .
View SolutionTwo cells, of voltage 10 V and 2 V and internal resistances 10Ω and 5Ω respectively, are connected in parallel as shown in Fig. Find the effective voltage and effective resistance of the combination.
View SolutionThree batteries of emf 4,5 and 6V and internal resistances 1,2 and 3Ω respectively are connected in parallel with each other and the combination sends a current through an external resistance of 4Ω. Find current drawn through each battery.
View Solution