In a balanced metre bridge, the segment of wire opposite to a resistance of 70Ω is 70 cm. The unknown resistance is
30Ω
60Ω
90Ω
15Ω
The correct Answer is:A
To solve the problem, we will use the principle of a balanced meter bridge. The relationship between the resistances and the lengths of the segments on the bridge is given by the formula:
R1R2=L1L2
where:
- R1 is the known resistance (70 Ω),
- R2 is the unknown resistance (which we need to find),
- L1 is the length of the wire segment opposite to R1 (70 cm),
- L2 is the length of the wire segment opposite to R2.
Since the total length of the meter bridge is 100 cm, we can find L2 as follows:
L2=100cm−L1=100cm−70cm=30cm
Now we can substitute the known values into the formula:
70ΩR2=70cm30cm
Cross-multiplying gives:
70Ω×30cm=R2×70cm
Now, simplifying this equation:
2100Ω⋅cm=R2×70cm
Dividing both sides by 70 cm:
R2=2100Ω⋅cm70cm=30Ω
Thus, the unknown resistance R2 is:
30Ω
- R1 is the known resistance (70 Ω),
- R2 is the unknown resistance (which we need to find),
- L1 is the length of the wire segment opposite to R1 (70 cm),
- L2 is the length of the wire segment opposite to R2.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NIKITA PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Multiple Choice Questions
314 Videos
- COMMUNICATION SYSTEMSBOOK - NIKITA PUBLICATIONCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Multiple Choice Questions (Examples for Practice)
8 Videos
- ELASTICITYBOOK - NIKITA PUBLICATIONCHAPTER - ELASTICITYEXERCISE - MCQ
314 Videos
Similar Questions
In the circuit a meter bridge a shown in the balanced state .The meter bridge wire has a resistance of 1Ω/cm. Calculate the unknown resistance Y and the current drawn from the battery of negiligible internal resistance
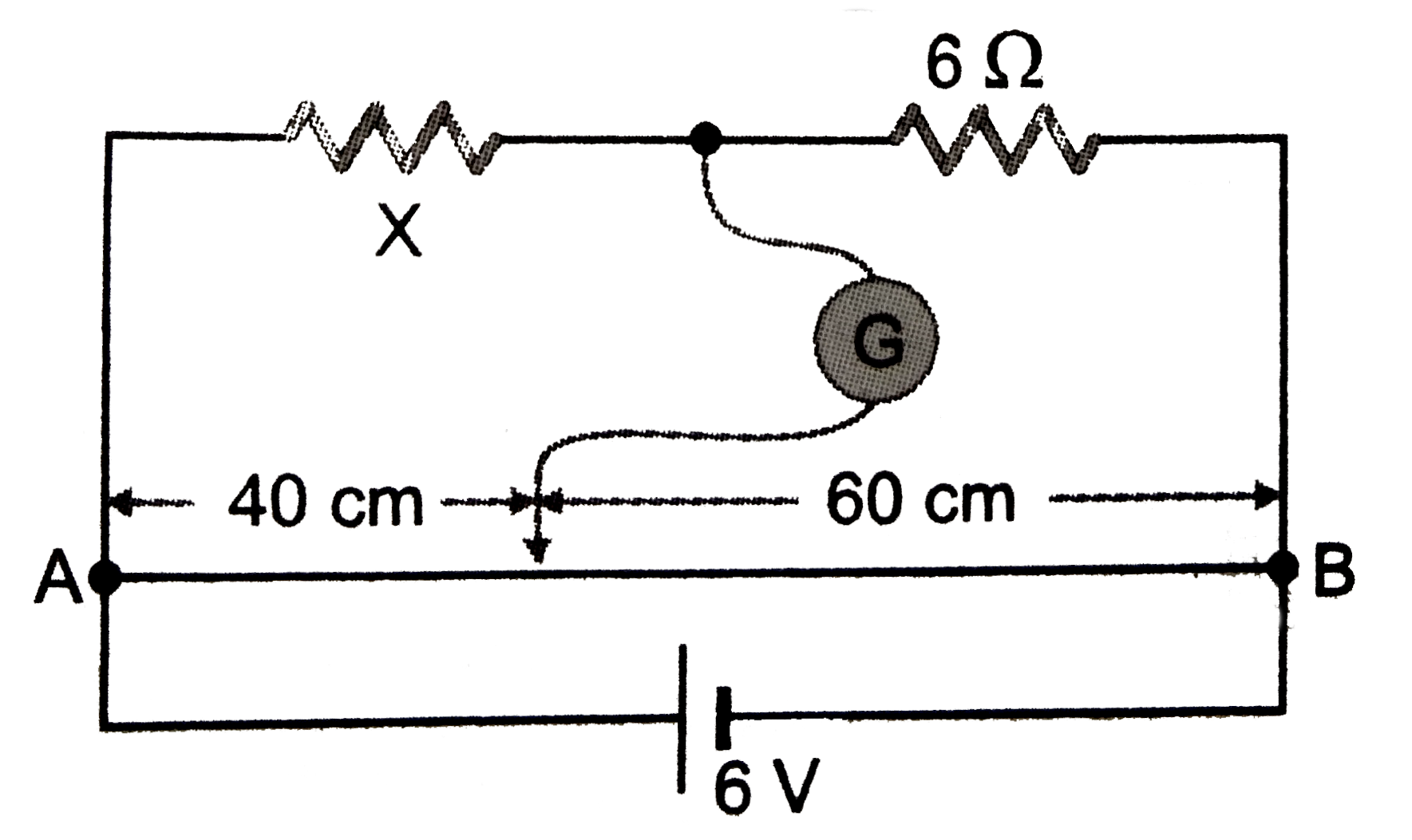
View SolutionIn the gives circuit, a meter bridge is shows in a balanced state. The bridge wire has a resistance of 1Ωcm−1. Find the value of the unknown resistance X and the current draws from the battery of negligible internal resistance.

View Solution
Knowledge Check
In balanced meter bridge, the resistance of bridge wire is 0.1Ωcm . Unknown resistance X is connected in left gap and 6Ω in right gap, null point divides the wire in the ratio 2:3 . Find the current drawn the battery of 5V having negligible resistance
A1AB1.5AC2AD5AIn the circuit shown, a meter bridge is in its balanced state. The meter bridge wire has a resistance .1ohm/cm. The value of unknown resistance X and the current drawn from the battery of negligible resistance is
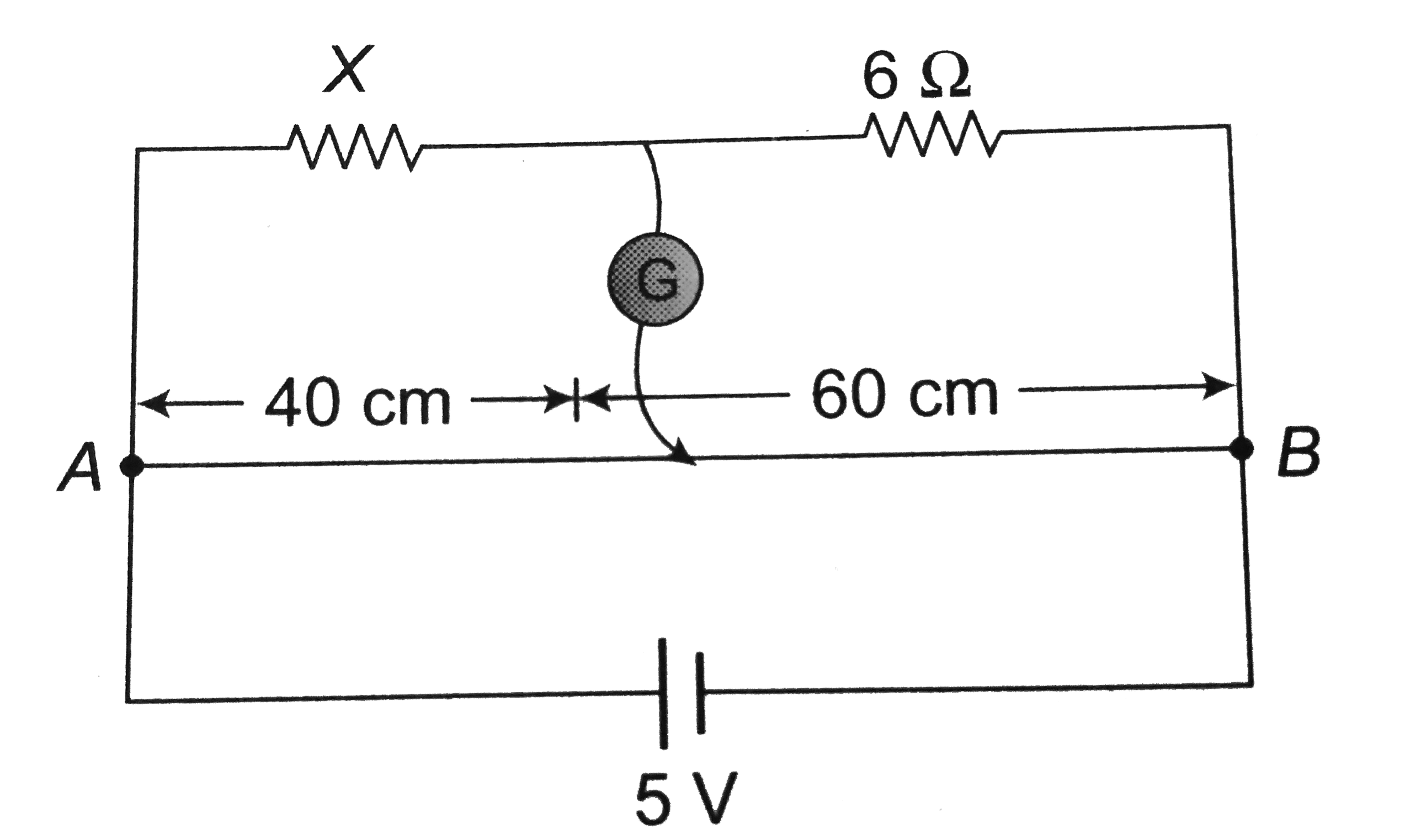 A6Ω,5ampB10Ω,0.1ampC4Ω,1.0ampD12Ω,0.5amp
A6Ω,5ampB10Ω,0.1ampC4Ω,1.0ampD12Ω,0.5ampIn a metre bridge experiment, unknown resistance X and known resistance of 60Ω is connected in left and right gap of a metre bridge respectively. If the null point is obtained at 40 cm from the left end then the unknown resistance is
A20ΩB40ΩC60ΩD80Ω
In the given circuit a bridge is shown in the balanced state.The meter bridge wire has a resistance of 1Ωcm−1 .Calculate the unknown resistance X and the current drawn from the battery of negligible internal resistence. If the magnitude the position of galvanometer and the cell, how it will affect the position of the galvanometer ?

View Solution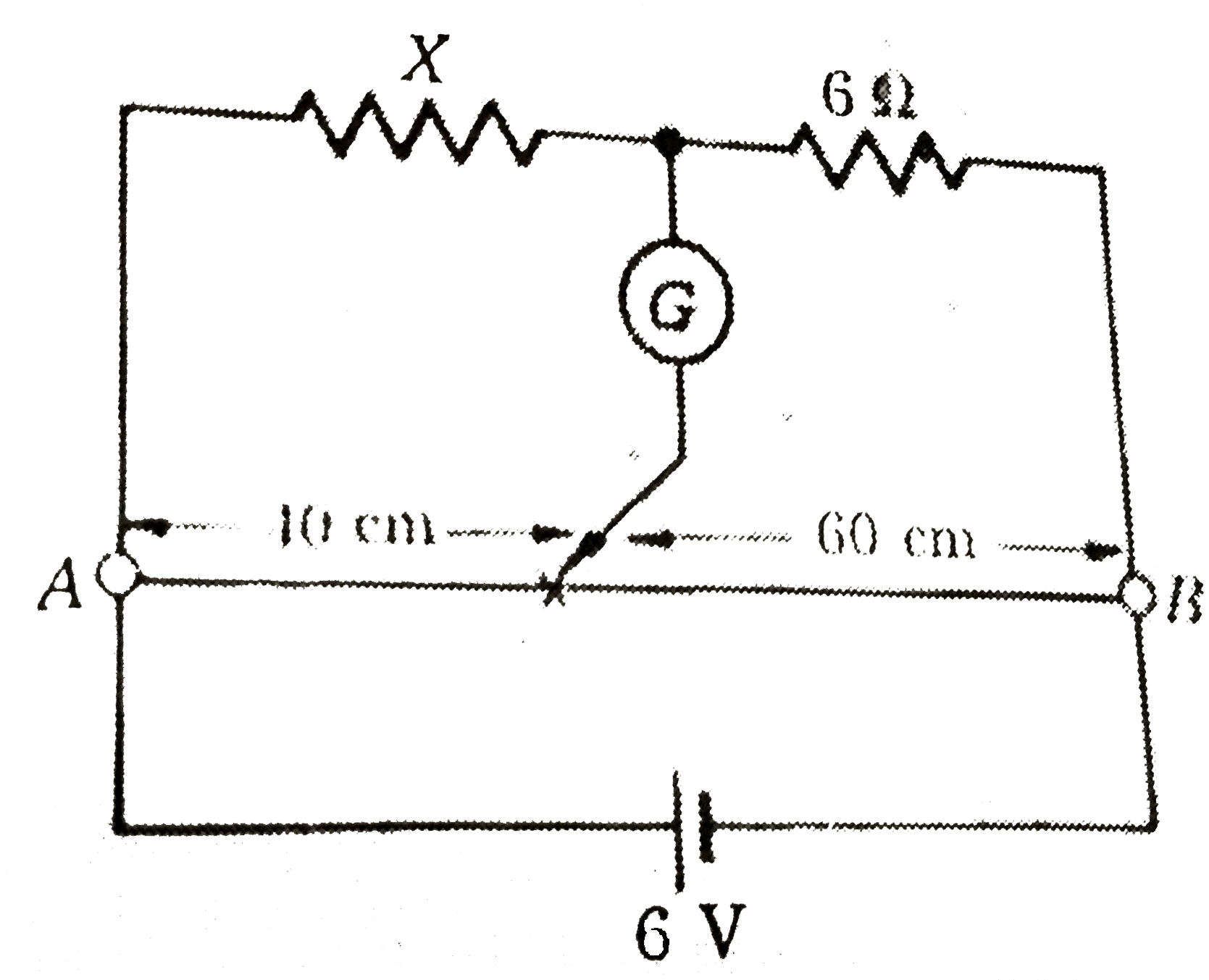
In the circuit shown in figure. A metre bridge is shown in its balanced state. The metre bridge wire has a resistance of a 4 ohm/cm. calculate the value of the unknown resistance X and the current drawn from the battery of negligible resistance.
View SolutionIn the following circuit, a metre bridge is shown in its balanced state. The metre bridge wire has a resistance of 1 ohm/cm. calculate the value of the unknown resistance X and the current drawn from the battery of negligible internal resistance.
View SolutionAn unknown resistance is connected in a left gap of a metre bridge . The balance point is obtained when a resistance of 10Ω is taken out from the resistance box in the right gap. On increasing the resistance from the resistance box by 12.5Ω the balance point shifts by 20 cm.
find the unknown resistance.
View SolutionIn the circuit shows in Fig. 6.20, a meter bridge is in its balance state. The meter bridge wire has a resistance of 1Ωcm−1. Calculate the value of the unknow resistance X and the battery of negligible internal resistance.
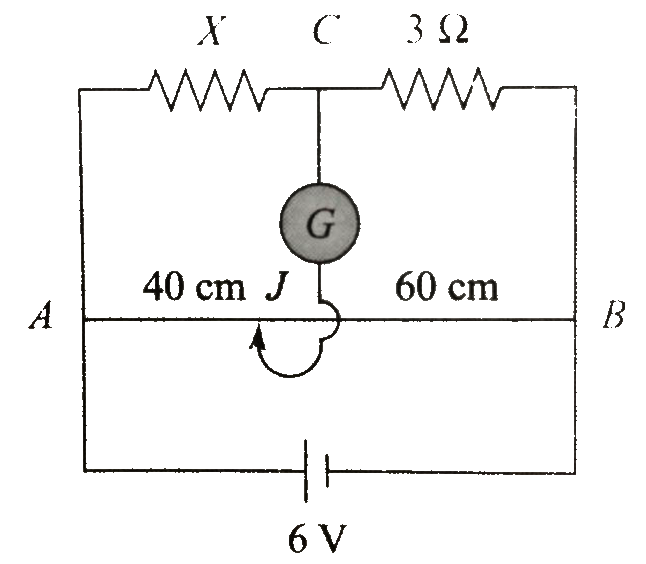
View Solution
