In an LCR series circuit the current is
in phase with applied emf
lags the applied voltage
lead the applied voltage
may lead or lag behind the applied voltage
The correct Answer is:D
To solve the problem regarding the current in an LCR series circuit, we need to understand the relationships between the voltage across the inductor (L), capacitor (C), and resistor (R), as well as how they relate to the total current in the circuit.
1. Understanding the Circuit:
In an LCR series circuit, we have an inductor (L), a capacitor (C), and a resistor (R) connected in series to an AC voltage source. The same current (I) flows through all components.
2. Voltage Relationships:
- The voltage across the resistor (Vr) is in phase with the current (I).
- The voltage across the inductor (VL) leads the current by 90 degrees (or π/2 radians).
- The voltage across the capacitor (VC) lags behind the current by 90 degrees (or π/2 radians).
3. Phase Diagram:
- We can represent these voltages as vectors (phasors) in a phase diagram.
- The voltage across the inductor (VL) is represented as a vector pointing upwards (leading).
- The voltage across the capacitor (VC) is represented as a vector pointing downwards (lagging).
- The voltage across the resistor (Vr) is represented as a vector along the horizontal axis (in phase).
4. Resultant Voltage:
- The total voltage (V) in the circuit can be found by vector addition of these voltages.
- If VL > VC, the resultant voltage vector will lead the current, indicating that the circuit is inductive.
- If VC > VL, the resultant voltage vector will lag behind the current, indicating that the circuit is capacitive.
- If VL = VC, the circuit is at resonance, and the total voltage is in phase with the current.
5. Resonance Condition:
- The resonance condition occurs when the inductive reactance (XL) equals the capacitive reactance (XC), i.e., XL=XC.
- At resonance, the circuit behaves purely resistively, and the current is in phase with the total voltage.
6. Conclusion:
- In an LCR series circuit, the current can either lead or lag depending on the relationship between VL and VC.
- At resonance, the current is in phase with the voltage.
Final Answer:
The current in an LCR series circuit can lead, lag, or be in phase with the total voltage depending on the values of the inductor and capacitor. The current is in phase when the inductive reactance equals the capacitive reactance (resonance condition).
In an LCR series circuit, we have an inductor (L), a capacitor (C), and a resistor (R) connected in series to an AC voltage source. The same current (I) flows through all components.
- The voltage across the resistor (Vr) is in phase with the current (I).
- The voltage across the inductor (VL) leads the current by 90 degrees (or π/2 radians).
- The voltage across the capacitor (VC) lags behind the current by 90 degrees (or π/2 radians).
- We can represent these voltages as vectors (phasors) in a phase diagram.
- The voltage across the inductor (VL) is represented as a vector pointing upwards (leading).
- The voltage across the capacitor (VC) is represented as a vector pointing downwards (lagging).
- The voltage across the resistor (Vr) is represented as a vector along the horizontal axis (in phase).
- The total voltage (V) in the circuit can be found by vector addition of these voltages.
- If VL > VC, the resultant voltage vector will lead the current, indicating that the circuit is inductive.
- If VC > VL, the resultant voltage vector will lag behind the current, indicating that the circuit is capacitive.
- If VL = VC, the circuit is at resonance, and the total voltage is in phase with the current.
- The resonance condition occurs when the inductive reactance (XL) equals the capacitive reactance (XC), i.e., XL=XC.
- At resonance, the circuit behaves purely resistively, and the current is in phase with the total voltage.
- In an LCR series circuit, the current can either lead or lag depending on the relationship between VL and VC.
- At resonance, the current is in phase with the voltage.
The current in an LCR series circuit can lead, lag, or be in phase with the total voltage depending on the values of the inductor and capacitor. The current is in phase when the inductive reactance equals the capacitive reactance (resonance condition).
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In an LCR series ac circuit, the current is
Aalways in phase with the voltageBlags the generator voltageCleads the generator voltageDnone of these - Question 2 - Select One
In LCR series AC circuit, the current
Ais always in phase with voltageBalways lags behind the generator voltageCalways leads the generator voltageDmay be in phase, lag behind or lead by the generator voltage depending on the values of L,C and R - Question 3 - Select One
Assertion : At resonance, LCR series circuit have a minimum current.
Reason : At resonance, in LCR series circuit, the current and e.m.f. are not in phase with each other.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
The phase difference between voltage and current in an LCR series circuit is
View SolutionIn a series LCR circuit
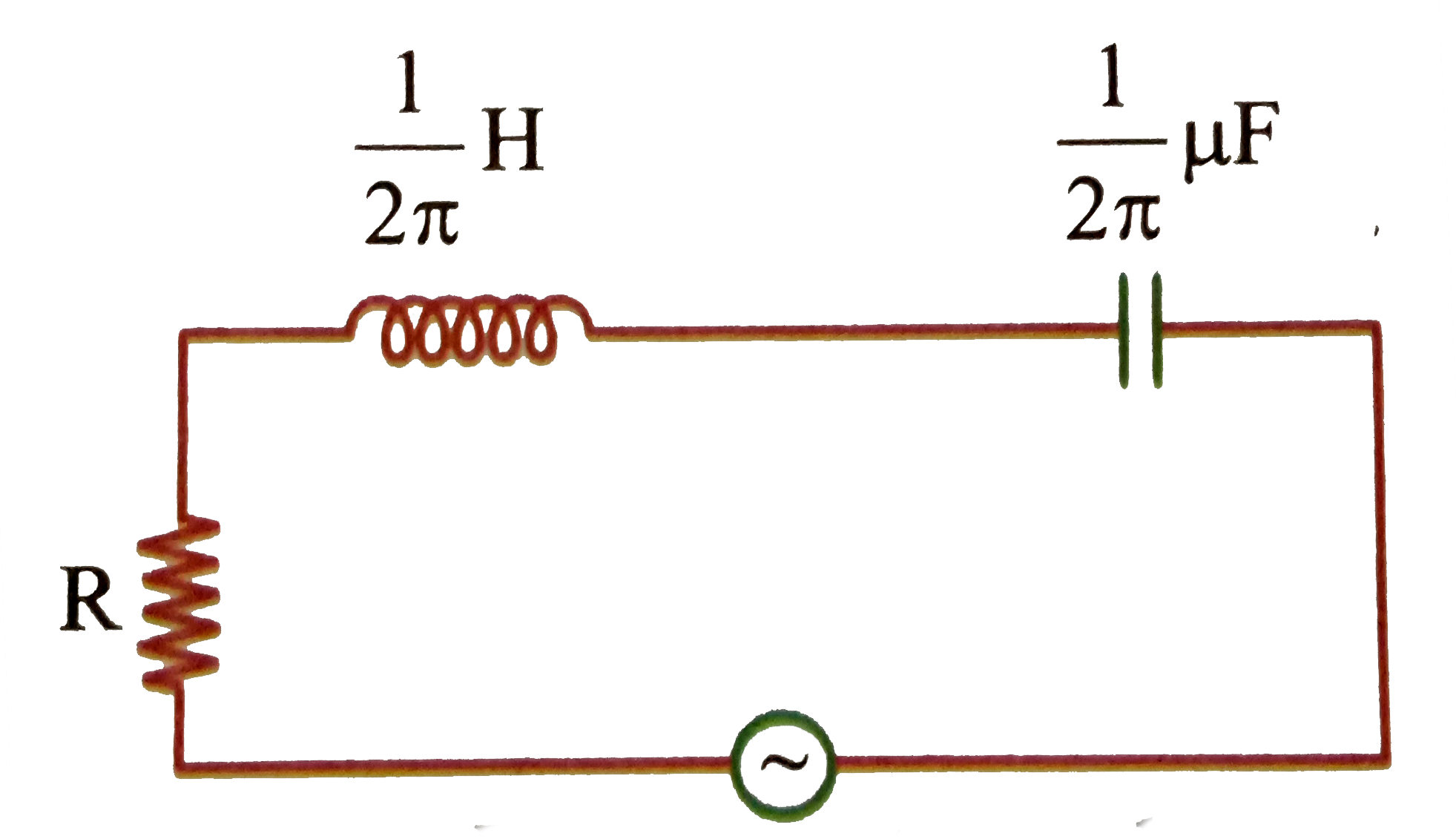 View Solution
View SolutionIn a LCR series circuit, if the phase difference between applied voltage and current is zero then
View SolutionIn LCR series circuit if the frequency is increased, the impendance of the circuit
View SolutionTo reduce the resonant frequency in an LCR series circuit with a generator
View Solution

