The path length of oscillation of simple pendulum of length 1 m is 16 cm. Its maximum velocity is (take, g=π2m/s2)
2πcm/s
4πcm/s
8πcm/s
16πcm/s
The correct Answer is:C
Data:
Path length (2a)=16cm
a=8cm
T=2π√1g−2π√1π2=2π×1π=2s
Vm=aω
=a×2πT=8×2π2
=8πcm/s.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
IF the length of a simple pendulum is increased, its maximum velocity during oscillation
AdecreasesBincreasesCremains sameDis zero - Question 2 - Select One
A simple pendulum 50cm long is suspended from the roof of a acceleration in the horizontal direction with constant acceleration √3gm/s−1. The period of small oscillations of the pendulum about its equilibrium position is (g=π2m/s2) ltbRgt
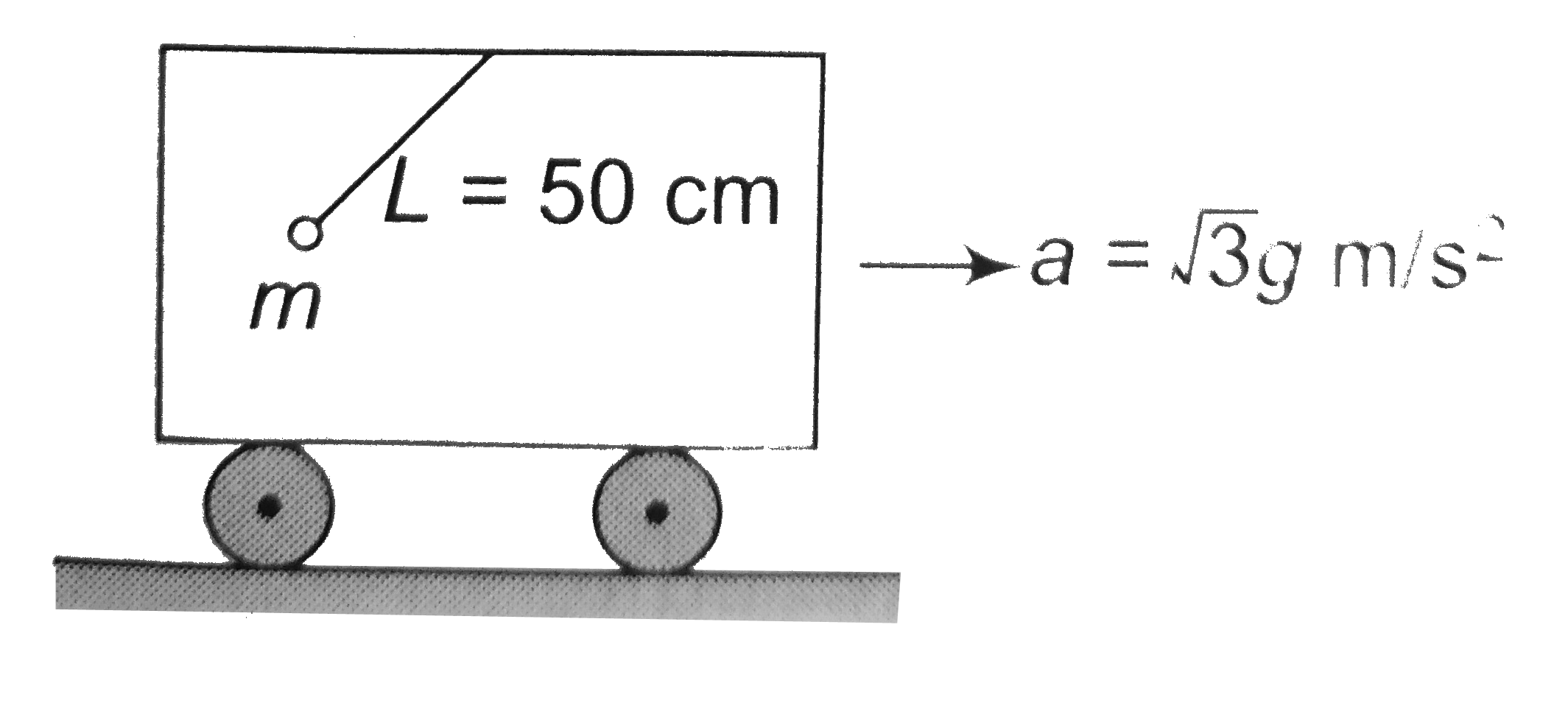 A1.0secB1.25secC1.53secD1.68sec
A1.0secB1.25secC1.53secD1.68sec - Question 3 - Select One
A graph is drawn between the displacement and time taken for the oscillations of a simple pendulum is 2s. The length of the penddulum is _______ m ( if g = 10 s−2andπ2=10)
A2B1C0.5D0.25
The time period of a simple pendulum of length 1 m is _____ second. ( take π2=10.g=10ms−2)
View SolutionFor oscillation of a simple pendulum of length L what is the maximum possible velocity at the lowest position What happens to the motion if velocity exceeds this value ?
View SolutionThe time t of a complete oscillation of a simple pendulum of length l is given by the equation T=2π√1g
where g is constant. What is the percentage error in T when l is increased by 1%?View SolutionA graph is drawn between the displacement and time taken for the oscillations of a simple pendulum. The length of the penddulum is _______ m ( if g = 10 s−2andπ2=10)
View SolutionA simple pendulum is taken at a place where its separation from the earth's surface is equal to the radius of the earth. Calculate the time period of small oscillation if the length of the string is 1.0m. Take g=π2m/s2 at the surface of the earth.
View Solution

