D(f+g)=
R−[−2,0)
R−[−1,0)
[−2,12]
none of these
The correct Answer is:b
Topper's Solved these Questions
- MAPPING OR FUNCTIONBOOK - CHHAYA PUBLICATIONCHAPTER - MAPPING OR FUNCTIONEXERCISE - Sample questions (Assertion -Reason type C)
3 Videos
- MAPPING OR FUNCTIONBOOK - CHHAYA PUBLICATIONCHAPTER - MAPPING OR FUNCTIONEXERCISE - Sample questions (Matrix Match type C)
2 Videos
- LOGARITHM BOOK - CHHAYA PUBLICATIONCHAPTER - LOGARITHM EXERCISE - Long Answer Type Question
12 Videos
- MATHEMATICAL REASONING BOOK - CHHAYA PUBLICATIONCHAPTER - MATHEMATICAL REASONING EXERCISE - JEE Main (AIEEE) Archive (2016 )
1 Videos
Similar Questions
If f(x)andg(f) are two differentiable functions and g(x)≠0 , then show that f(x)g(x) is also differentiable ddx{f(x)g(x)}=g(x)ddx{f(x)}−f(x)ddx{g(x)}[g(x)]2
View SolutionIf f(x)andg(f) are two differentiable functions and g(x)≠0 , then show trht f(x)g(x) is also differentiable ddx{f(x)g(x)}=g(x)dx{f(x)}−g(x)dx{g(x)}[g(x)]2
View Solution
Knowledge Check
If f(x)=ax+b and g(x)=cx+d, then f(g(x))=g(f(x)) is equivalent to
Af(a)=g(c)Bf(b)=g(b)Cf(d)=g(b)Df(c)=g(a)Let f(x) = ax + b and g(x)= cx+ d. Then f (g(x)) = g (fex) is equivalent to:
Af(c) = g(a)Bf(a) = g(c)Cf(c) = g(d)Df(d) = g(b)
If f(x)=ax+b and g(x)=cx+d, then f(g(x))=g(f(x)) is equivalent to (A) f(a) = g(c ) (B) f(b) = g(b) (C) f(d) = g(b) (D) f(c ) = g(a)
View Solutiona.
 b.
b. 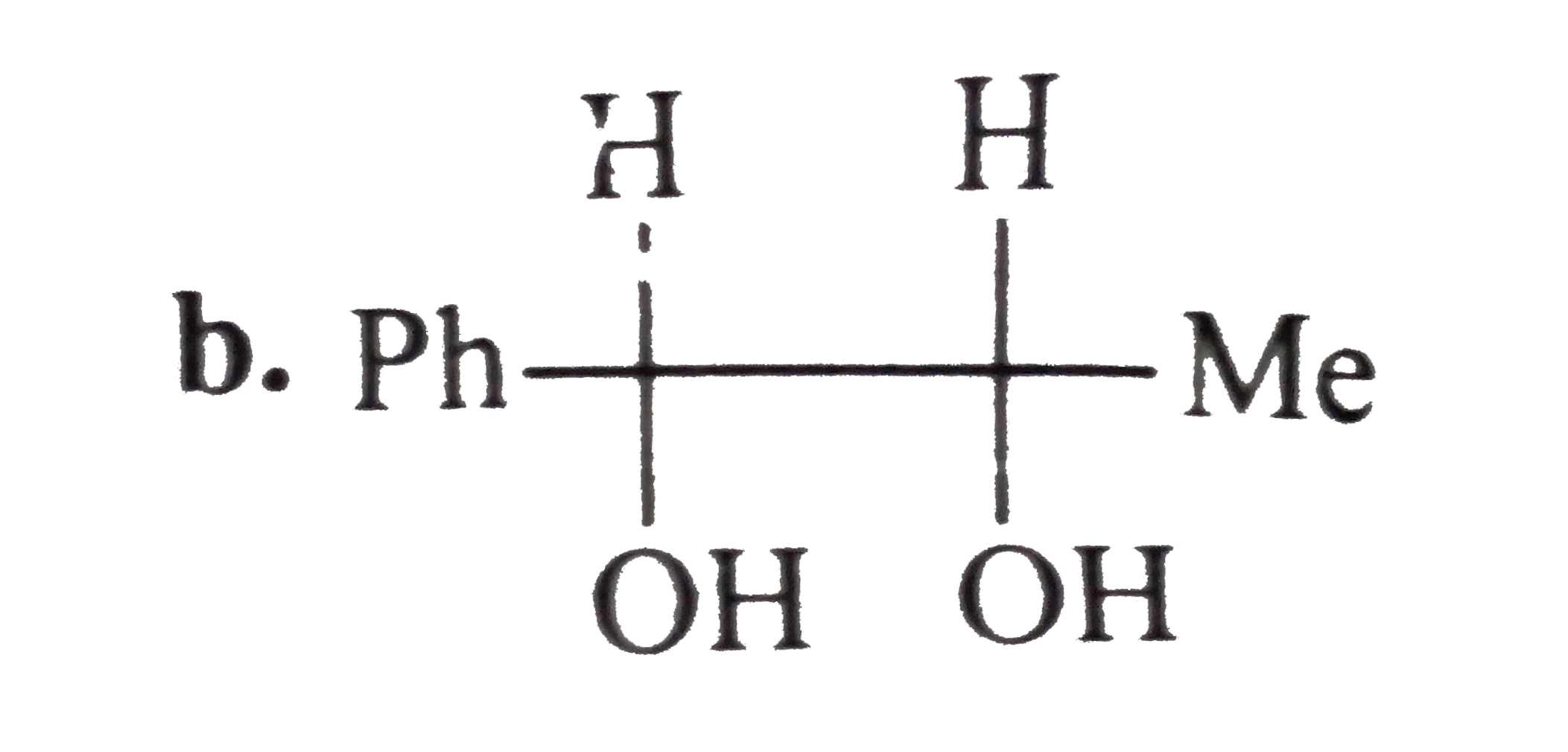
c.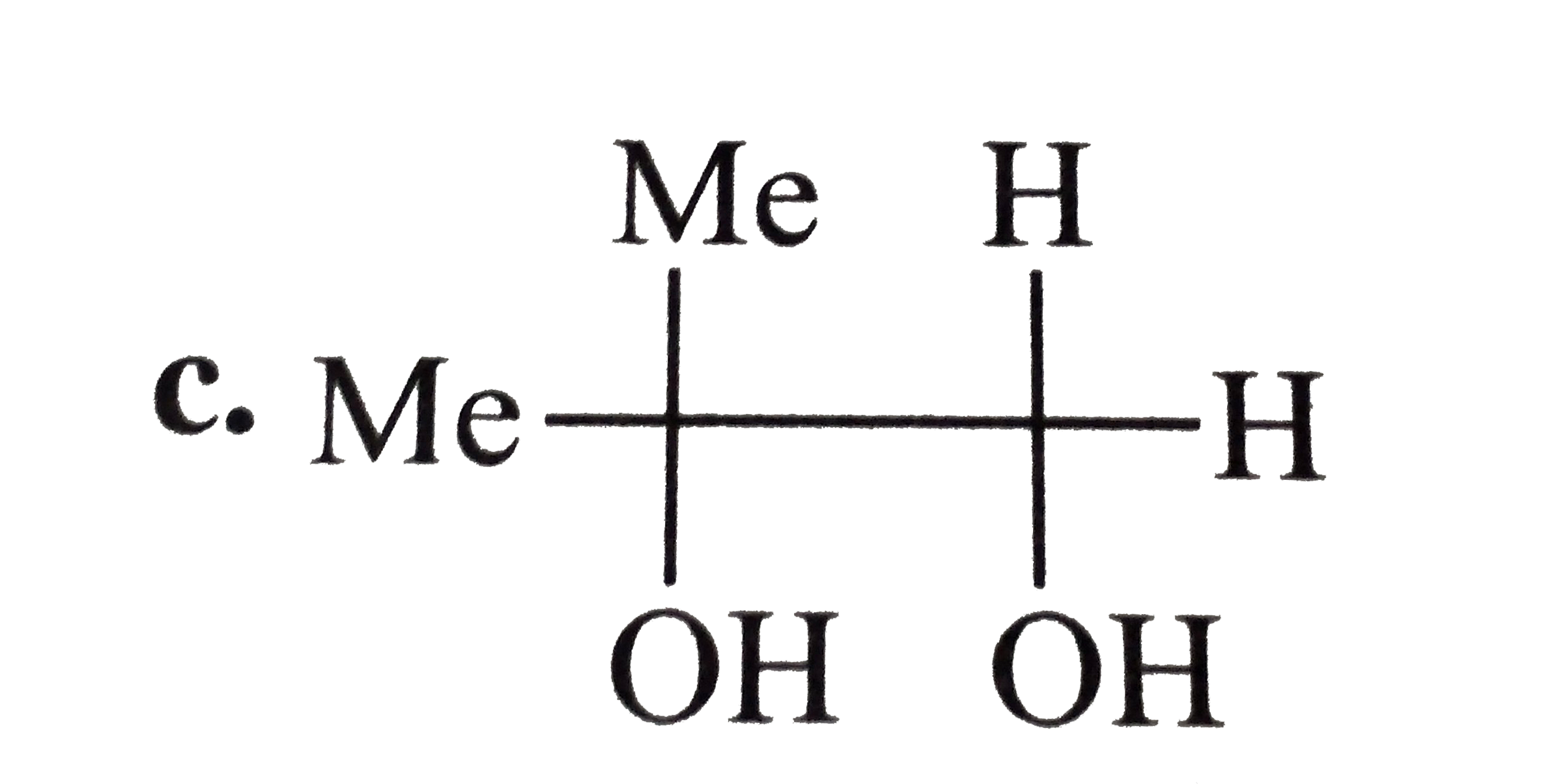 d.
d. 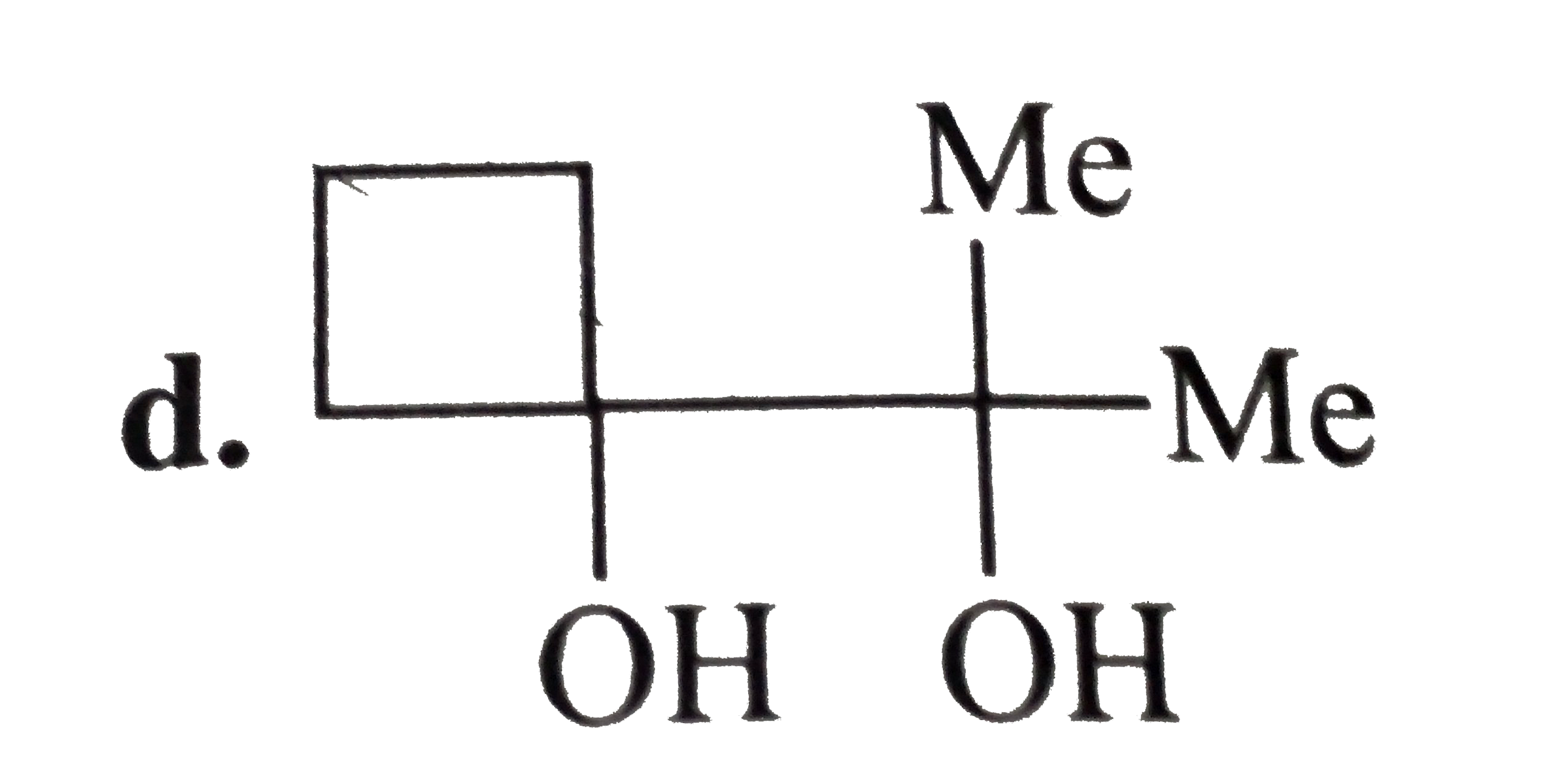
e.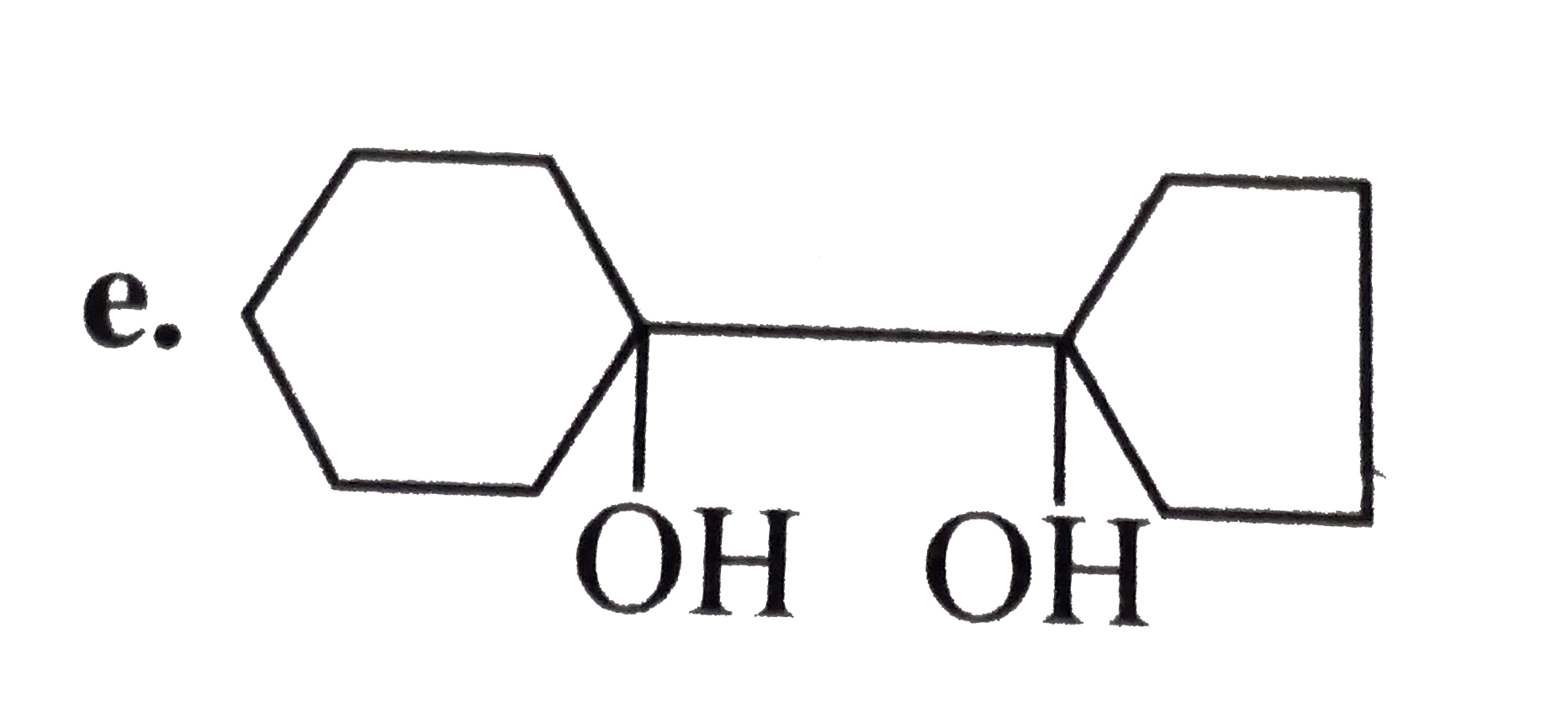 f.
f. 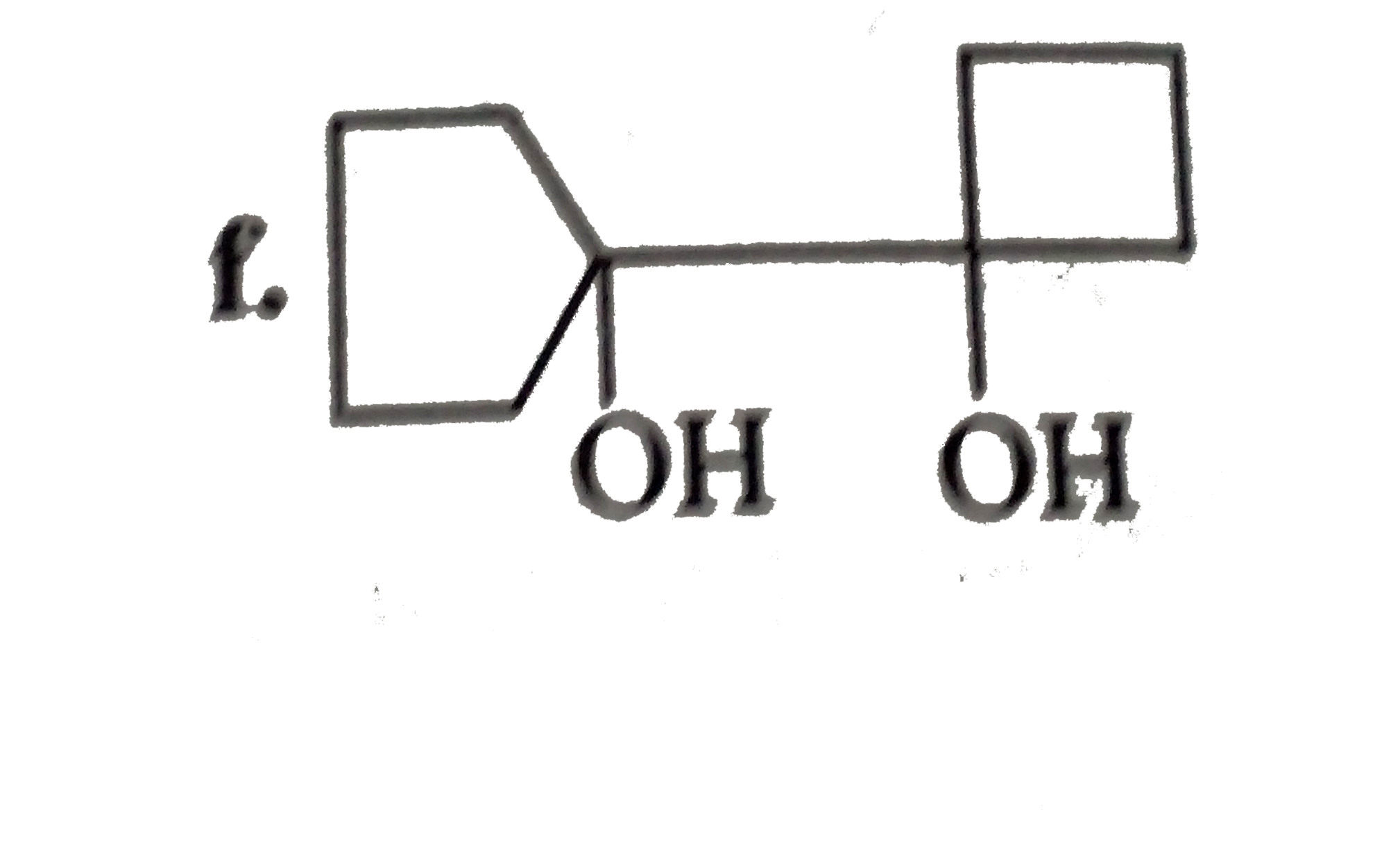
g.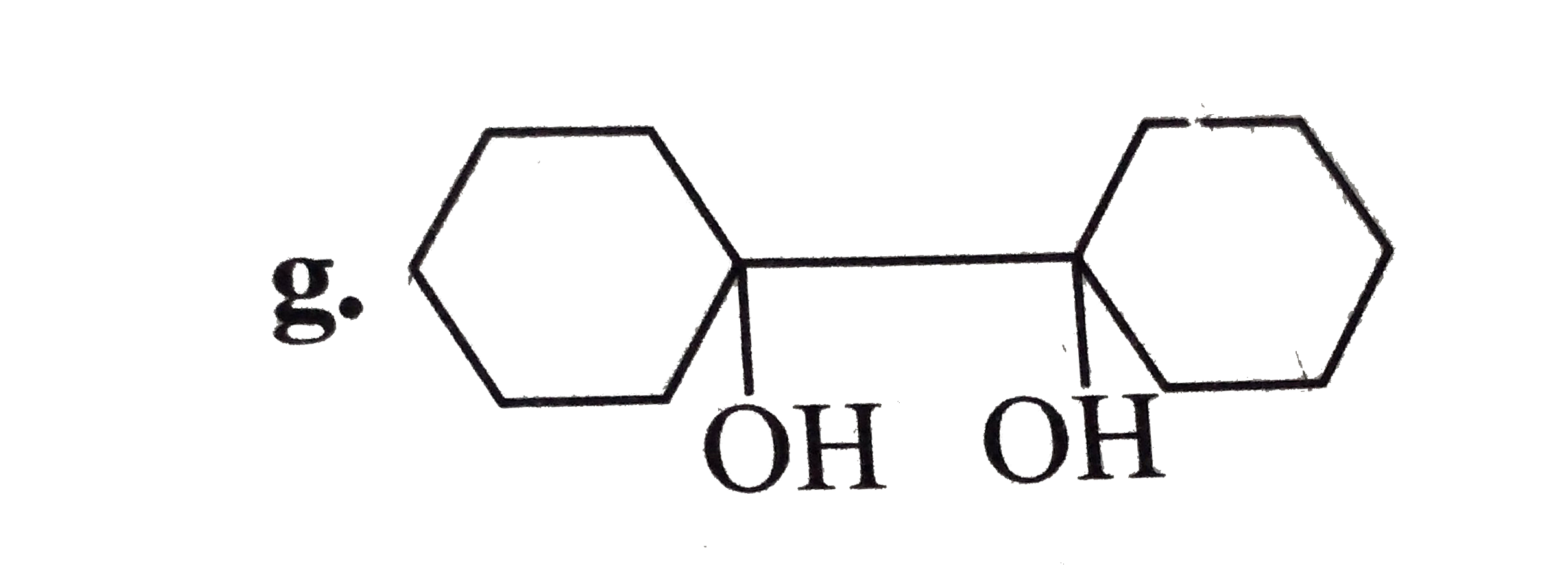 h.
h. 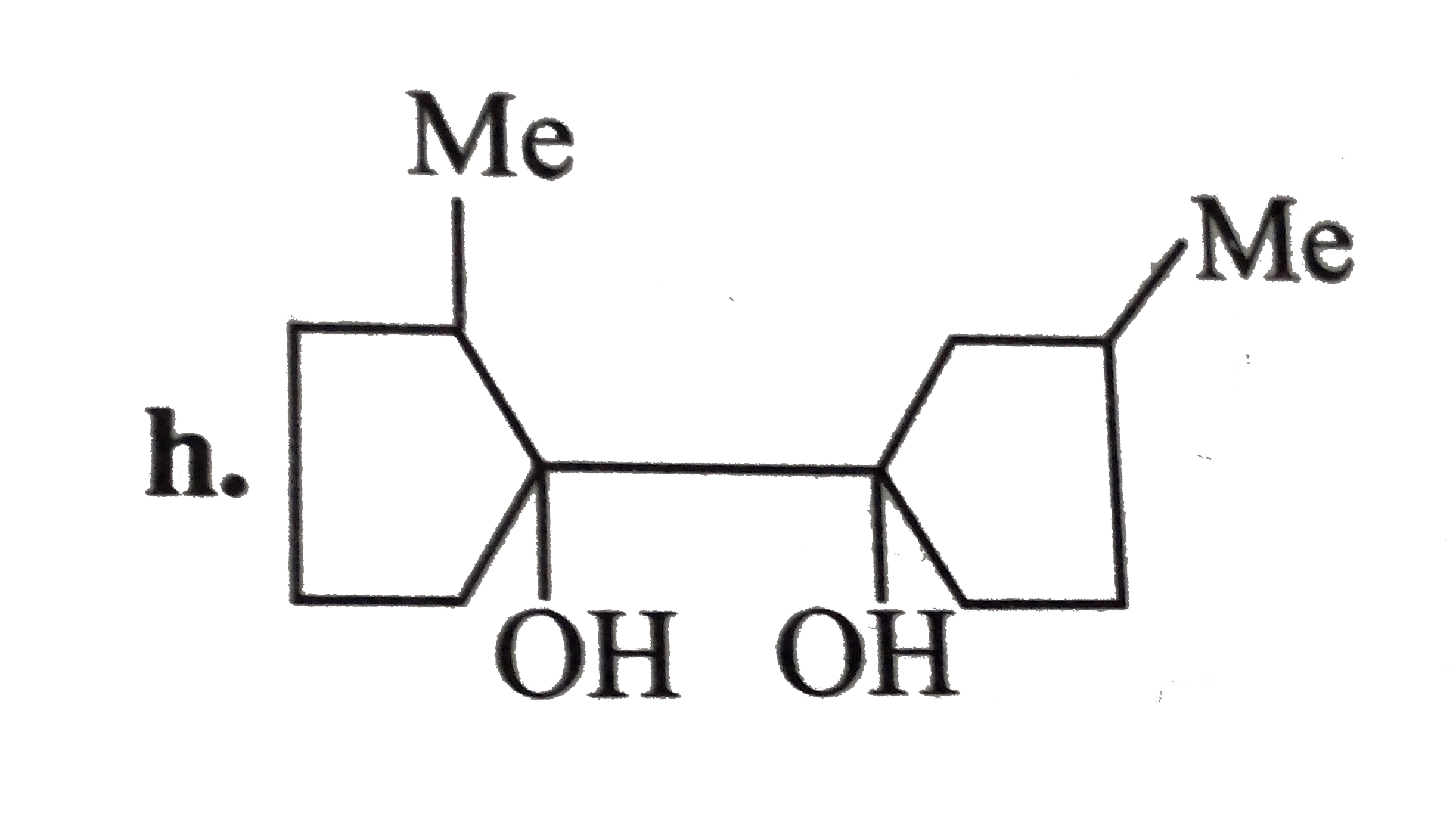
View SolutionIn Figure, DEFG is a square and ∠BAC=90 . Prove that (i) A G F ~ D B G(ii)AGF~EFC (iii) D B G ~ E F C(iv)DE2=BDxEC
View SolutionIf f(x) and g(x) are differentiable function ; then show that f(x)±g(x) are also differentiable such that df(x)±g(x)dx=df(x)dx±dg(x)dx
View SolutionIn Fig. 4.128, DEFG is a square and ∠BAC=90o . Prove that AGFDBG (ii) AGFEFC (FIGURE) (iii) DBGEFC (iv) DE2=BD×EC
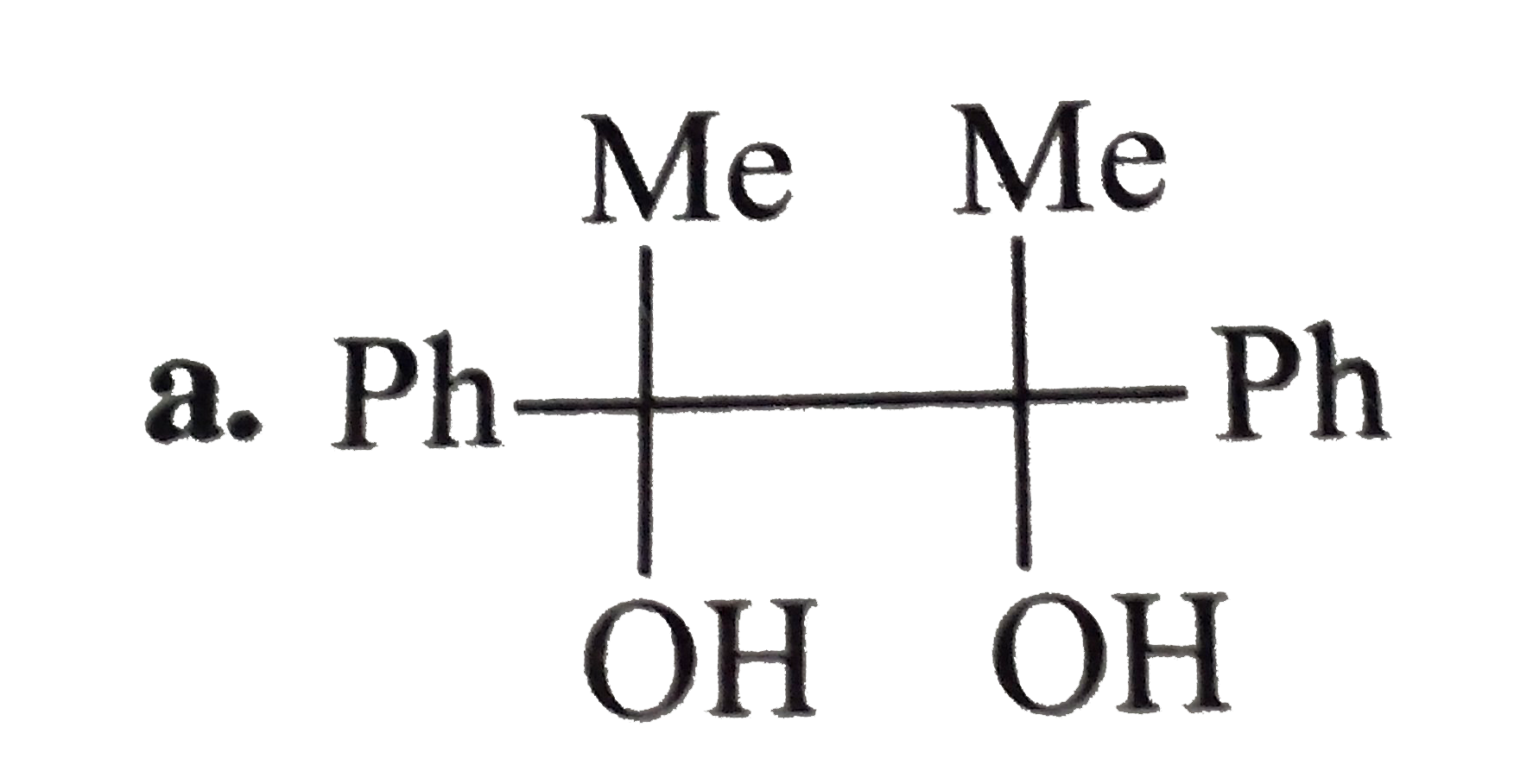
View SolutionDistinguish between the following:
a.
b.
c.
d.
e.
f.
g.
View Solution
