The system of equation<br> x+y+2z=1,x+2y+3z=2,x+4y+αz=4. Has unique then Solution in Bengali
α≠3
α≠5
α≠2
α≠1
The correct Answer is:B
Step by step video, text & image solution for The system of equation x+y+2z=1, x+2y+3z=2, x+4y+alphaz=4. Has unique then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ADJOINT AND INVERSE OF A MATRIX AND SOLUTION OF LINEAR SIMULTANEOUS EQUATIONS BY MATRIX METHODBOOK - CHHAYA PUBLICATIONCHAPTER - ADJOINT AND INVERSE OF A MATRIX AND SOLUTION OF LINEAR SIMULTANEOUS EQUATIONS BY MATRIX METHODEXERCISE - MATRIX MATCH TYPE
2 Videos
- ADJOINT AND INVERSE OF A MATRIX AND SOLUTION OF LINEAR SIMULTANEOUS EQUATIONS BY MATRIX METHODBOOK - CHHAYA PUBLICATIONCHAPTER - ADJOINT AND INVERSE OF A MATRIX AND SOLUTION OF LINEAR SIMULTANEOUS EQUATIONS BY MATRIX METHODEXERCISE - COMPERHENSION TYPE
6 Videos
- ADJOINT AND INVERSE OF A MATRIX AND SOLUTION OF LINEAR SIMULTANEOUS EQUATIONS BY MATRIX METHODBOOK - CHHAYA PUBLICATIONCHAPTER - ADJOINT AND INVERSE OF A MATRIX AND SOLUTION OF LINEAR SIMULTANEOUS EQUATIONS BY MATRIX METHODEXERCISE - MULTIPLE CORRECT ANSWER TYPE
5 Videos
- ALGEBRABOOK - CHHAYA PUBLICATIONCHAPTER - ALGEBRAEXERCISE - JEE ADVANCED ARCHIVE 2016
5 Videos
Similar Questions
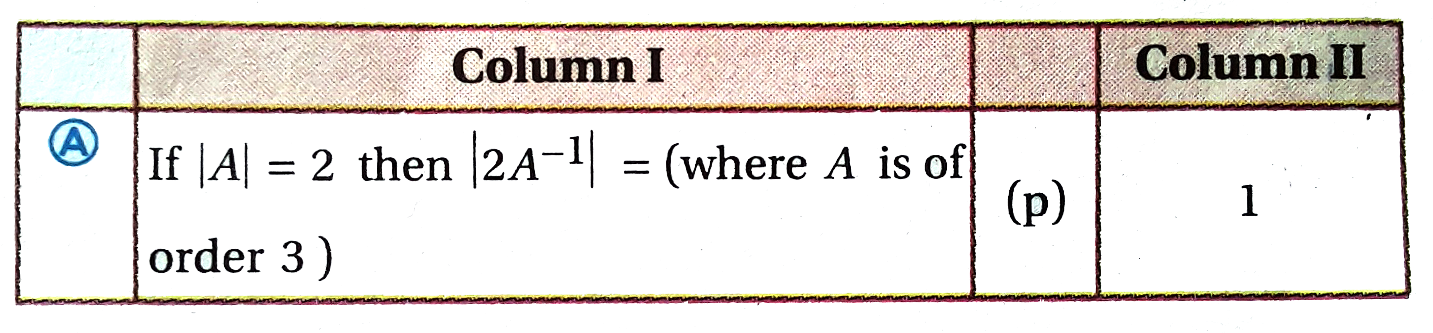

View SolutionTwo n×n square matrices A and B are said to be similar if there exists a non - singular matrix C such that C−1 AC = B .
If A and B are two singular matrices, then-
View SolutionIf A is a matrix of size n×n such that A2+A+2I = O then
View SolutionLet p=⎡⎢⎣3−1−220α3−50⎤⎥⎦, where α∈R. Suppose Q=[qij] is a matrix such that PQ=kl, where k∈R,k≠0andl is the identity matrix of order 3. If q23=−k8anddet(Q)=k22, then
View SolutionUsing matrices, solve the following system of equations : x+2y−3z=6,3x+2y−2z=3,2x−y+z=2
View SolutionIf the system of equations x+2y+3z=4,x+py+2z=3,x+4y+z=3 has an infinite number of solutions and solution triplet is
View SolutionConsider the system of equations
x+y+z=6
x+2y+3z=10
x+2y+λz=μ
the system has unique solution if
View SolutionThe solution of the system of equations is x−y+2z=1,2y−3z=1 and 3x−2y+4y=2 is
View Solutionगुणन (Use product) का प्रयोग समीकरण निकाय (to solve the system of equations) को हल करने के लिए करे,
x−y+2z=1,2y−3z=1,3x−2y+4z=2
View SolutionIf the system of equations x+ y + z = 5 , x+2y+3z=9, x+3y+αz=β has unique solution, then value of α can’t be:
View SolutionThe system of equations x+y+z=6,x+2y+3z=14,x+4y=7z=30 has
View SolutionIf the system of equation
x+y+2z=3,x+2y+3z=4andx+cy+2xz=5 is inconsistent, then
View SolutionThe number of Solutions of the system of equations 2x+y−z=7,x−3y+2z=1,x+4y−3z=5 is
View SolutionFor a unique value of αandβ, then system of equations given by x+y+z=6,x+2y+3z=14 and 2x+5y+αz=β ,has infinitely many solutions,then |α−β| is
View SolutionThe value of λ for which the system of equations :
x+y+z=6,x+2y=3z=10,x+4y+λz=12 has a unique solution is :
View Solution
