A square matrix A is used to be an idempotent matrix if A2=A.
If A is a non-singular idempotent matrix, then-Solution in Bengali
A =In
A=0
A + A' =0
none of these
The correct Answer is:A
Step by step video, text & image solution for A square matrix A is used to be an idempotent matrix if A^(2) = A. If A is a non-singular idempotent matrix, then- by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ADJOINT AND INVERSE OF A MATRIX AND SOLUTION OF LINEAR SIMULTANEOUS EQUATIONS BY MATRIX METHODBOOK - CHHAYA PUBLICATIONCHAPTER - ADJOINT AND INVERSE OF A MATRIX AND SOLUTION OF LINEAR SIMULTANEOUS EQUATIONS BY MATRIX METHODEXERCISE - ASSERTION-REASON TYPE
2 Videos
- ADJOINT AND INVERSE OF A MATRIX AND SOLUTION OF LINEAR SIMULTANEOUS EQUATIONS BY MATRIX METHODBOOK - CHHAYA PUBLICATIONCHAPTER - ADJOINT AND INVERSE OF A MATRIX AND SOLUTION OF LINEAR SIMULTANEOUS EQUATIONS BY MATRIX METHODEXERCISE - MATRIX MATCH TYPE
2 Videos
- ALGEBRABOOK - CHHAYA PUBLICATIONCHAPTER - ALGEBRAEXERCISE - JEE ADVANCED ARCHIVE 2016
5 Videos
Similar Questions
If A = [3+2ii−i3−2i] then find A−1
View Solution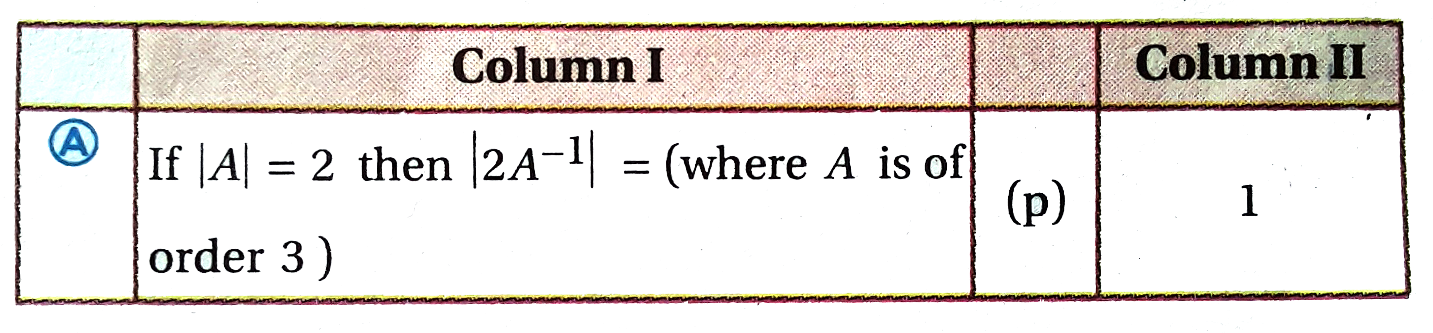

View SolutionLet p=⎡⎢⎣3−1−220α3−50⎤⎥⎦, where α∈R. Suppose Q=[qij] is a matrix such that PQ=kl, where k∈R,k≠0andl is the identity matrix of order 3. If q23=−k8anddet(Q)=k22, then
View SolutionIdempotent Matrix
View SolutionSome special square matrices are defined as follows. Nilpotent matrix: A square matrix. A is said to be nilpotent (of order 2)if, A2=O. A square matrix is said to be nilpotent of order p, if p is the least positive integer such that Ap=O.
Idempotent matrix: A square matrix A is said to be idempotent if, A2=A.
e.g.[1001] is an idempotent matrix.
Involutory matrix: A square A is said to be involutary if A2=I, Ibeing the identity matrix.
e.g..A=[1001] is an involutary matrix.
Orthogonal matrix: A square matrix A is said to be an orthogonal matrix if A'A=I=AA'
The matrix A ⎡⎢⎣113526−2−1−3⎤⎥⎦
View SolutionIf B is an idempotent matrix, and A=I−B, then
View SolutionIf A is an idempotent matrix, then show that B=l-A is also idempotent and AB=BA=0
View SolutionA square matrix A is used to be an idempotent matrix if A2=A.
If A is an idempotent matrix and B = I -A, then-
View SolutionA square matrix A is used to be an idempotent matrix if A2=A.
If A, B and A + B are idempotent matrices, then-
View SolutionIf A≠I is an idempotent matrix, then A is a
View SolutionA matrix A is said to be an Idempotent matrix if A2=A. Then which of the following is true
View SolutionIf A^2 = I, then matrix A is Orthogonal matrix Idempotent matrix Involutory matrix Nilpotent matrix
View Solutionএকটি বর্গ ম্যাট্রিক্স A-কে বর্গেকসম ম্যাট্রিক্স বলা হবে যদি A2=A হয়। যদি A-নন-সিঙ্গুলার বর্গেকসম ম্যাট্রিক্স হয় তবে-
View SolutionLet A be 3×3 matrix such that A is orthogonal idempotent then
View SolutionIf A is a non-singular matrix such that AAT=ATA and B=A−1AT, the matrix B is a. involuntary b. orthogonal c. idempotent d. none of these
View Solution
