The eccentricity of the hyperbola 2x=a(t+1t),2y=a(t−1t)Solution in Bengali
2
3
√2
2√2
The correct Answer is:C
Step by step video, text & image solution for The eccentricity of the hyperbola 2x = a(t + (1)/(t)), 2y = a(t-(1)/(t)) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HYPERBOLABOOK - CHHAYA PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - VERY SHOT ANSWER TYPE QUESTIONS
16 Videos
- HYPERBOLABOOK - CHHAYA PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
1 Videos
- HYPERBOLABOOK - CHHAYA PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - SAMPLE QUESTIONS FOR COMPETITIVE EXAMS
12 Videos
- DIAGRAMMATIC REPRESENTATION OF DATABOOK - CHHAYA PUBLICATIONCHAPTER - DIAGRAMMATIC REPRESENTATION OF DATAEXERCISE - EXERCISE (Very short Answer Type Question)
7 Videos
- MATHEMATICAL INDUCTION BOOK - CHHAYA PUBLICATIONCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Sample Questions for Competitive Exams
20 Videos
Similar Questions
Explain what geometrical diagrams are represented by the equatio x2a2+y2a2(1−e2)=1, where a and e are constants.
View SolutionFind the coordinates of the foci of the rectangular hyperbola x2−y2=9
View SolutionThe equation px2+2qxy+ry2+2sx+2ty+u=0 (where p≠q≠r and p,q,r,s,t and u are constants ) represents-
View SolutionThe following table gives the frequency distribution of heights in inches of a group of 100 peple:
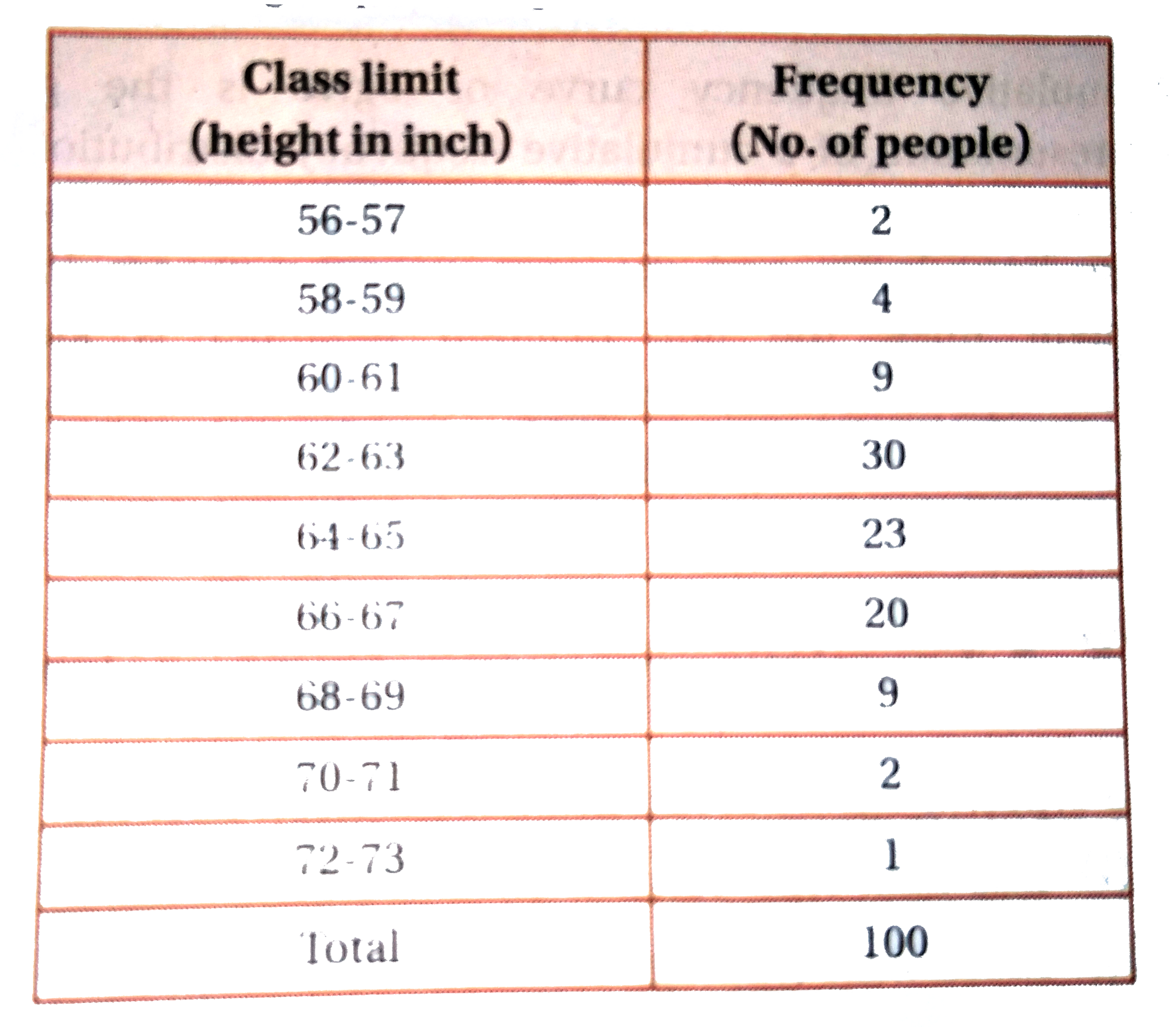 Draw a histogram for height distribution. Shade the portion of the histogram which will represent the total number of people whose heights lie between 60.5 and 66.5 inches.
Draw a histogram for height distribution. Shade the portion of the histogram which will represent the total number of people whose heights lie between 60.5 and 66.5 inches.
View SolutionIf for all n∈N and n≥1, then (32n−1) is always divisible by
View SolutionThe locus of point ((e^(t)+e^(-t))/(2),(e^(t)-e^(-t))/(2)) is a hyperbola with eccentricity
View SolutionThe eccentricity the hyperbola x=a2(t+1t),y=a2(t−1t) is a.√2 . b. √3 c. 2√3 d. 3√2
View SolutionIf t is a variable parameter, show that x=a2(t+1t)andy=b2(t−1t) represent a hyperbola.
View SolutionShow that for all values of t the point x = a. 1+t21−t2,y=2at1−t2lies on a fixed hyperbola. What is the value of the eccentricity of the hyperbola?
View SolutionProve that the point {a2(t+1t),b2(t−1t)} lies on the hyperbola for all values of t(t≠0).
View SolutionThe eccentricity of the hyperbola x=a2(t+1/t),y=a2(t−1/t) is
View SolutionThe locus of the point (et+e−t2,et−e−t2) is a hyperbola of eccentricity
View SolutionThe eccentricity of the conic x=3((1-t^(2))/(1+t^(2))) and y=(2t)/(1+t^(2)) is
View SolutionFind the eccentricity of the hyperbola given by equations x=et+e−t2 and y=et−e−t3,t∈R.
View SolutionFind the eccentricity of the hyperbola given by equations x=et+e−12andy=et−e−13,t∈R.
View Solution
