Find (i) the length of axes (ii) length of latus rectum (iii) coordianates of vertices (iv) eccentricity (v) coordinates of foci and (vi) equations of the directries of each of the following hyperbolas:
(a) 4x2−9Y2=36 (b) 9y2−25x2=225Solution in Bengali
The correct Answer is:(a) 6 and 4 (ii) 83 (iii) (±3,0) (iv) √133 (v) (±√13,0) (vi) √13x=±9
(b) (i) 10 and 6 (ii) 185 (iii) (0,±5) (iv) √345 (v) (0,±√34) (vi) √34y=±25
Step by step video, text & image solution for Find (i) the length of axes (ii) length of latus rectum (iii) coordianates of vertices (iv) eccentricity (v) coordinates of foci and (vi) equations of the directries of each of the following hyperbolas: (a) 4x^(2) - 9Y^(2) = 36 (b) 9y^(2) - 25x^(2) = 225 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HYPERBOLABOOK - CHHAYA PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - LONG ANSWER TYPE
10 Videos
- HYPERBOLABOOK - CHHAYA PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - SAMPLE QUESTIONS FOR COMPETITIVE EXAMS
12 Videos
- HYPERBOLABOOK - CHHAYA PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
1 Videos
- DIAGRAMMATIC REPRESENTATION OF DATABOOK - CHHAYA PUBLICATIONCHAPTER - DIAGRAMMATIC REPRESENTATION OF DATAEXERCISE - EXERCISE (Very short Answer Type Question)
7 Videos
- MATHEMATICAL INDUCTION BOOK - CHHAYA PUBLICATIONCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Sample Questions for Competitive Exams
20 Videos
Similar Questions
Find the centre, the length of latus rectum, the eccentricity, the coordinates of foci and the equations of the directrices of the hyperbola (x+2)29−(y−1)216=1.
View SolutionThe equation px2+2qxy+ry2+2sx+2ty+u=0 (where p≠q≠r and p,q,r,s,t and u are constants ) represents-
View SolutionFind the coordinates of the foci of the rectangular hyperbola x2−y2=9
View SolutionThe following table gives the frequency distribution of heights in inches of a group of 100 peple:
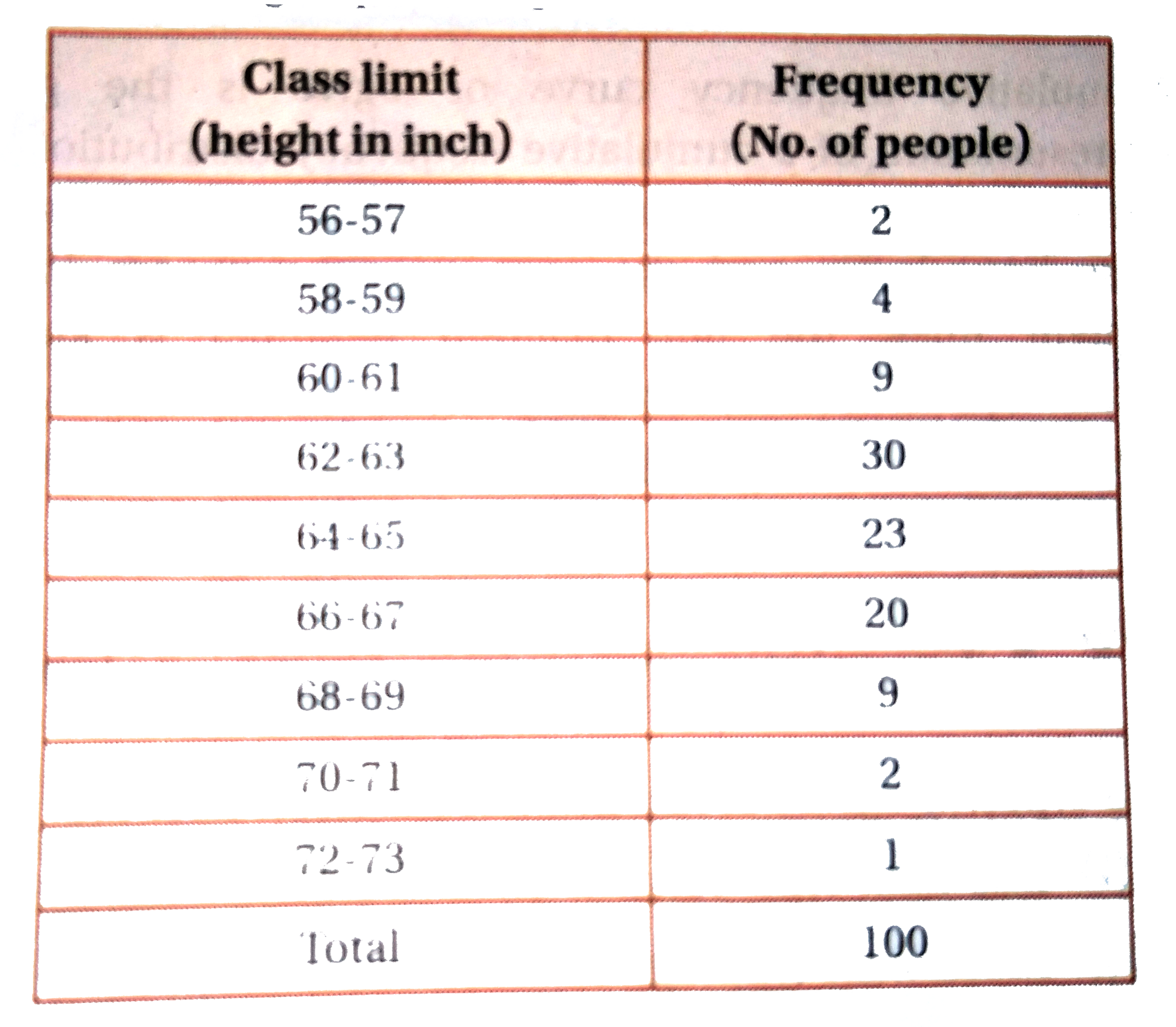 Draw a histogram for height distribution. Shade the portion of the histogram which will represent the total number of people whose heights lie between 60.5 and 66.5 inches.
Draw a histogram for height distribution. Shade the portion of the histogram which will represent the total number of people whose heights lie between 60.5 and 66.5 inches.
View SolutionIf for all n∈N and n≥1, then (32n−1) is always divisible by
View SolutionFind the coordinates of the foci and the vertices, the eccentricity and the length of the latus rectum of the hyperbolas.9y2−4x2=36
View SolutionIn the hyperbola 4x2−9y2=36, find the axes, the coordinates of the foci, the eccentricity, and the latus rectum.
View SolutionFind the coordinates of the foci, the vertices, the eccentricity and the length of the latus rectum of the Hyperbola 9y2−4x2=36
View SolutionFind (a) the lengths of the major and minor axes (b) the length of latus rectum (c) coordinates of vertices (d) eccentricity (e) coordinates of foci and (f) the equations of directrices for the following ellipse :
25x2+9y2=225
View SolutionIn each of the find the coordinates of the foci and the vertices, the eccentricity and the length of the latus rectum of the hyperbolas.
9y2−4x2=36
View SolutionIn each of the find the coordinates of the foci and the vertices, the eccentricity and the length of the latus rectum of the hyperbolas. 16x^(2)-9y^(2)=576
View SolutionIn each of the find the coordinates of the foci and the vertices, the eccentricity and the length of the latus rectum of the hyperbolas.
9y2−4x2=36
View SolutionIn each of the find the coordinates of the foci and the vertices, the eccentricity and the length of the latus rectum of the hyperbolas. 16x^(2)-9y^(2)=576
View SolutionFind the coordinates of the foci and the vertices, the eccentricity and the length of the latus rectum of the hyperbola.
9y2−4x2=36
View SolutionIn each of the find the coordinates of the foci and the vertices, the eccentricity and the length of the latus rectum of the hyperbolas.
9y2−4x2=36
View Solution
