e1ande2 are respectively the eccentricites of a hyperbola and its conjugate. Prove that 1e21+1e22=1Solution in Bengali
Step by step video & image solution for e_(1) and e_(2) are respectively the eccentricites of a hyperbola and its conjugate. Prove that (1)/(e_1^(2))+(1)/(e_2^2) =1 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - LONG ANSWER TYPE10videos
HYPERBOLA
- BOOK - CHHAYA PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - SAMPLE QUESTIONS FOR COMPETITIVE EXAMS12videos
HYPERBOLA
- BOOK - CHHAYA PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS1videos
HYPERBOLA
- BOOK - CHHAYA PUBLICATIONCHAPTER - DIAGRAMMATIC REPRESENTATION OF DATAEXERCISE - EXERCISE (Very short Answer Type Question)7videos
DIAGRAMMATIC REPRESENTATION OF DATA
- BOOK - CHHAYA PUBLICATIONCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Sample Questions for Competitive Exams20videos
MATHEMATICAL INDUCTION
Similar Questions
Find the centre, the length of latus rectum, the eccentricity, the coordinates of foci and the equations of the directrices of the hyperbola (x+2)29−(y−1)216=1.
06:59View SolutionThe equation px2+2qxy+ry2+2sx+2ty+u=0 (where p≠q≠r and p,q,r,s,t and u are constants ) represents-
02:37View SolutionFind the coordinates of the foci of the rectangular hyperbola x2−y2=9
01:57View SolutionThe following table gives the frequency distribution of heights in inches of a group of 100 peple:
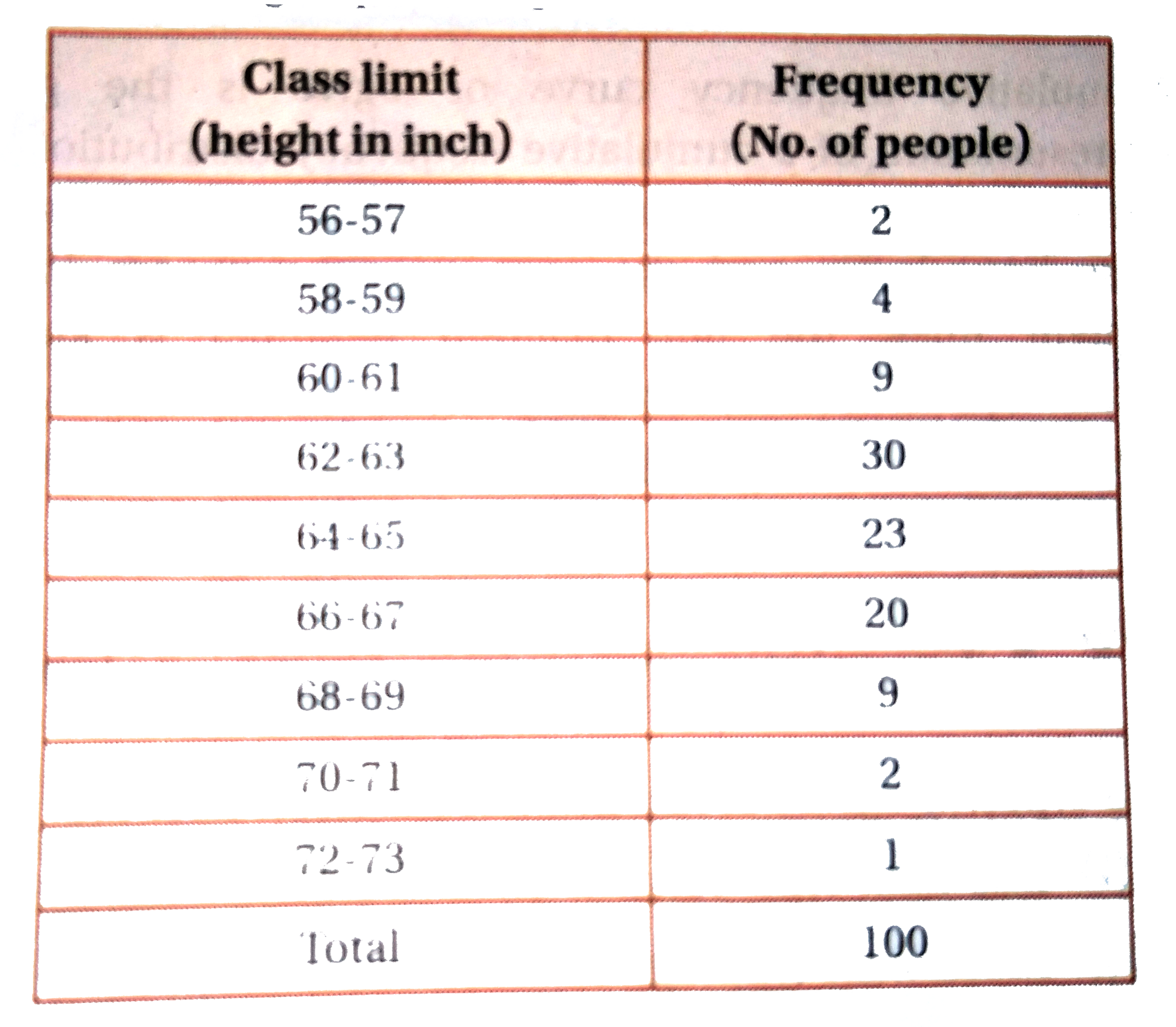Draw a histogram for height distribution. Shade the portion of the histogram which will represent the total number of people whose heights lie between 60.5 and 66.5 inches. 04:48View SolutionIf for all n∈N and n≥1, then (32n−1) is always divisible by
02:33View SolutionAn ellipse and a hyperbola are confocal (have the same focus) and the conjugate axis of the hyperbola is equal to the minor axis of the ellipse. If e1ande2 are the eccentricities of the ellipse and the hyperbola, respectively, then prove that 1e12+1e22=2 .
02:55View SolutionLet e1ande2 be the eccentricities of a hyperbola and its conjugate hyperbola respectively. Statement 1 : e1e2>√2. Statement 2 : 1e2_1+1e2_2=
04:04View SolutionIf e1 and e2 are the eccentricites of hyperbola xy=c2 and x2−y2=c2, then e21+e22=
02:30View SolutionIf e1ande2 are the eccentricities of a hyperbola 3x2−2y2=25 and its conjugate, then
01:46View SolutionIf e1 is the eccentricity of the hyperbola y2b2−x2a2=1 then e1 =
03:09View SolutionIf e1ande2 are the eccentricities of a hyperbola and its conjugate then prove that 1e21+1e22=1.
02:16View SolutionIf e1 be the eccentricity of a hyperbola and e2 be the eccentricity of its conjugate, then show that the point (1e1,1e2) lies on the circle x2+y2=1.
03:51View SolutionIf e1 and e2 are the eccentricities of the hyperbola and its conjugate hyperbola respectively then 1e21+1e22 is equal to
03:05View SolutionIf e1,e2 are the eccentricites of the hyperbla 2x2−2y2=1 and the ellipse x2+2y2=2 respectively then
03:40View Solutione1ande2 are eccentricities of hyperbola and conjugate hyperbola respectively then prove that 1e21+1e22=1.
05:36View Solution