A circle of radius r intersects a rectangular hyperbola whose centre is at C, at four points P,Q,R and S. If CP2+CQ2+CR2+CS2=ar2, then the value of'a' be -Solution in Bengali
The correct Answer is:4
Step by step video, text & image solution for A circle of radius r intersects a rectangular hyperbola whose centre is at C, at four points P,Q,R and S. If CP^(2)+ CQ^(2)+ CR^(2)+ CS^(2)=ar^(2), then the value of'a' be - by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - LONG ANSWER TYPE10videos
HYPERBOLA
- BOOK - CHHAYA PUBLICATIONCHAPTER - DIAGRAMMATIC REPRESENTATION OF DATAEXERCISE - EXERCISE (Very short Answer Type Question)7videos
DIAGRAMMATIC REPRESENTATION OF DATA
- BOOK - CHHAYA PUBLICATIONCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Sample Questions for Competitive Exams20videos
MATHEMATICAL INDUCTION
Similar Questions
Find the centre, the length of latus rectum, the eccentricity, the coordinates of foci and the equations of the directrices of the hyperbola (x+2)29−(y−1)216=1.
05:47View SolutionThe following table gives the frequency distribution of heights in inches of a group of 100 peple:
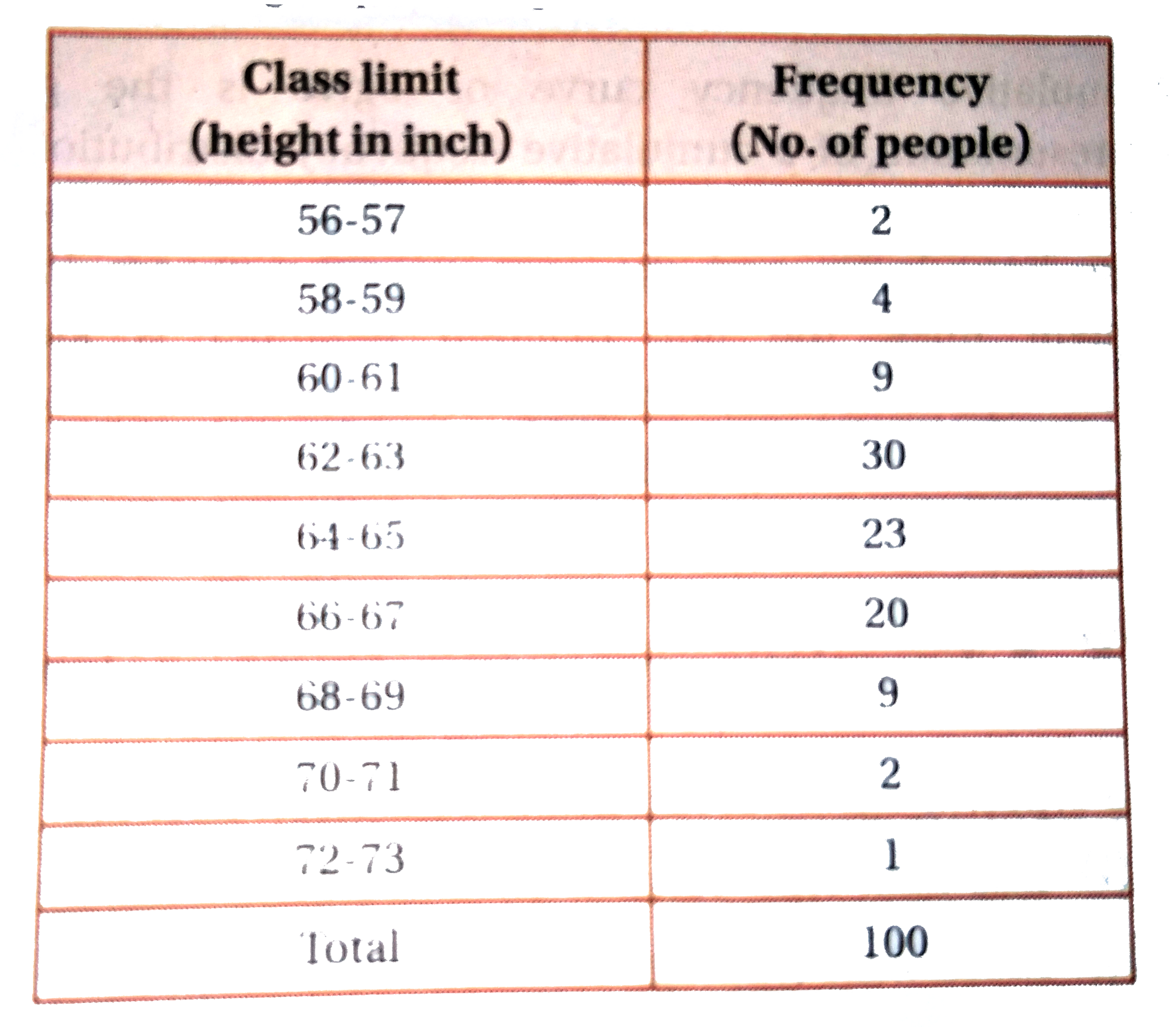Draw a histogram for height distribution. Shade the portion of the histogram which will represent the total number of people whose heights lie between 60.5 and 66.5 inches. 06:12View SolutionIf for all n∈N and n≥1, then (32n−1) is always divisible by
03:28View SolutionPQ and RS are two perpendicular chords of the rectangular hyperbola xy=c2. If C is the center of the rectangular hyperbola, then find the value of product of the slopes of CP,CQ,CR, and CS.
07:14View SolutionIf two points P&Q on the hyperbola (x^(2))/(a^(2))-(y^(2))/(b^(2))=1 whose centre is C be such that CP is perpendicularal to CQ and a
03:34View SolutionA rectangular hyperbola whose centre is C is cut by any circle of radius r in four points P,Q ,R and S. Then,CP^(2)+CQ^(2)+CR^(2)+CS^(2)=(A)r^(2)(B)2r^(2) (C) 3r^(2)(D)4r^(2)
06:33View SolutionIf two points P&Q on the hyperbola ,x2a2−y2b2=1 whose centre is C be such that CP is perpendicularal to CQanda<b1 ,then the value of 1CP2+1CQ2=
05:42View SolutionA rectangular hyperbola whose centre is C is cut by any circle of radius r in four points P,Q,R and S . Then CP^2+CQ^2+CR^2+CS^2 equals .
05:20View SolutionIf two points P&Q on the hyperbola ,x2a2−y2b2=1 whose centre is C be such that CP is perpendicularal to CQanda<b1 ,then prove that 1CP2+1CQ2=1a2−1b2.
10:44View SolutionIf two points P&Q on the hyperbola ,x2a2−y2b2=1 whose centre is C be such that CP is perpendicularal to CQanda<b1 ,then prove that 1CP2+1CQ2=1a2−1b2.
06:54View SolutionA rectangular hyperbola whose center is C intersects at four points PQ, and S by a circle of radius, then CP^(2) + CQ^(2) + CR^(2) + CS^(2) The value of
04:26View SolutionIf any tangent to the hyperbola x2a2−y2b2=1 with centre C, meets its director circle in P and Q, show that CP and CQ are conjugate semi-diameters of the hyperbola.
06:47View SolutionA rectangular hyperbola whose centre is C is cut by any circle of radius r in four points P, Q, R and S. Then, CP^2 +CQ^2 +CR^2 + CS^2 = (A) r^2 (B) 2r^2 (C) 3r^2 (D) 4r^2
04:49View SolutionIf two points P&Q on the hyperbola ,x2a2−y2b2=1 whose centre is C be such that CP is perpendicularal to CQanda<b1 ,then prove that 1CP2+1CQ2=1a2−1b2.
07:47View SolutionIf two points P & Q on the hyperbola , x^2/a^2-y^2/b^2=1 whose centre is C be such that CP is perpendicularal to CQ and a lt b 1 ,then prove that 1/(CP^2)+1/(CQ^2)=1/a^2-1/b^2 .
06:29View Solution