Two rods of same length and cross section are joined along the length. Thermal conductivities of first and second rod are K1 and K2. The temperature of the free ends of the first and second rods are maintained at θ1 and θ2 respectively. The temperature of the common junction isSolution in Tamil
θ1+θ22
K1K2K1+K2(θ1+θ2)
K1θ1+K2θ2K1+K2
K2θ1+K1θ2K1+K2
The correct Answer is:C
Step by step video, text & image solution for Two rods of same length and cross section are joined along the length. Thermal conductivities of first and second rod are K_1 and K_2. The temperature of the free ends of the first and second rods are maintained at θ_1 and θ_2 respectively. The temperature of the common junction is by Physics experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HEATBOOK - CHETAN PUBLICATIONCHAPTER - HEATEXERCISE - Explain the following / meaning of statement
11 Videos
- HEATBOOK - CHETAN PUBLICATIONCHAPTER - HEATEXERCISE - Open Ended Question:
3 Videos
- HEATBOOK - CHETAN PUBLICATIONCHAPTER - HEATEXERCISE - Distinguish between
3 Videos
- GRAVITATIONBOOK - CHETAN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - ASSIGNMENT-1
15 Videos
- LENSESBOOK - CHETAN PUBLICATIONCHAPTER - LENSESEXERCISE - Assignment
14 Videos
Similar Questions
Role of Latent heat in the change of state of a substances.
View SolutionWhile deciding the unit for heat , which temperature interval is chosen ? Why ?
View SolutionWhat is the difference between heat and temperature?
View SolutionThe value of g at the centre of the Earth is zero. Explain?
View SolutionThe defect of myopia can be corrected by using ___________ .
View SolutionOne end of a thermally insulated rod is kept at a temperature T_1 and the other at T_2 . The rod is composed of two sections of length l_1 and l_2 and thermal conductivities K_1 and K_2 respectively. The temperature at the interface of the two section is
View SolutionTwo rods A and B have lengths l_1 and l_2. Each rod has its ends at temperature T_1 and T_2 Radii fo cross section of the two rods are same. The condition for equal flow of heat through those two rods is (K_1, K_2 are thermal conductivities of two rods)
View SolutionTwo rods of different materials having differnet lengths and same cross sectional areas are joined end to end in a straight line. The free ends of this compound rod are maintained at different temperatures The temperature gradient in each rod will be .
View SolutionTwo rods of the same length and areas of cross-section A_1 and A_2 have their ends at the same temperature. K_1 and K_2 are the thermal conductivities of the two rods. The rate of flow of heat is same in both the rods if-
View SolutionTwo rods of same length and cross section are joined along the length. Thermal conductivities of first and second rod are K_(1) and K_(2) . The temperature of the free ends of the first and seconds rods are maintained at theta_(1) and theta_(2) respectively. The temperature of the common junction is
View SolutionTwo rods having thermal conductivity in the ratio of 5 : 3 having equal lengths and equal cross-sectional area are joined by face to face. If the temperature of the free end of the first rod is 100^(@)C and free end of the second rod is 20^(@)C . Then temperature of the junction is
View SolutionTwo rods A and B of different materials but same cross section are joined as in figure. The free end of A is maintained at 100°C and the free end of B is maintained at 0°C. If l_2=2l_1,K_1=2K_2 and rods are thermally insulated from sides to prevent heat loses then the temperature theta of the junction of the two rods is
View SolutionSteady state temperature are shown in the diagram. Find ratio of thermal conductivity k1k2 if length of all rods are same
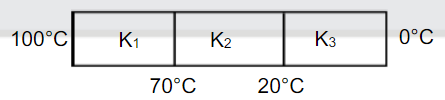
View SolutionTwo rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is
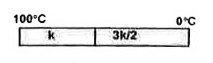
View SolutionSteady state temperature are shown in the diagram. Find ratio of thermal conductivity k1k2 if length of all rods are same

View Solution
