For s-orbitals, since (Psi orbitals wave function) is independent of a

Class 11 CHEMISTRY STRUCTURE OF ATOM

Topper's Solved these Questions

ATOMIC STRUCTUREBOOK - A2ZCHAPTER - ATOMIC STRUCTUREEXERCISE - Section B - Assertion Reasoning
34 Videos
ATOMIC STRUCTUREBOOK - A2ZCHAPTER - ATOMIC STRUCTUREEXERCISE - AIPMT/NEET Questions
59 Videos
ATOMIC STRUCTUREBOOK - A2ZCHAPTER - ATOMIC STRUCTUREEXERCISE - Heisenbergs Uncertainity Principle And Debroglie Equation
44 Videos
CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - A2ZCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Section D - Chapter End Test
30 Videos

Knowledge Check

The Schrodinger wave equation for H-atom is
$\nabla^{2} Ψ = \frac{8 π^{2} m}{h^{2}} (E - V) Ψ = 0$
Where $\nabla^{2} = \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} + \frac{\partial^{2}}{\partial z^{2}}$
E = Total energy and V=potential energy wave function $Ψ_{(\begin{matrix} r & θ & ϕ \end{matrix})} R_{(r)} Θ_{(θ)} Φ_{(ϕ)}$
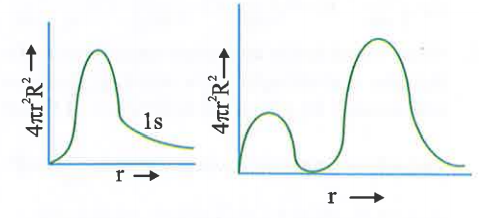
R is radial wave function which is function of ''r'' only, where r is the distance from nucleus. $Θ$ and $Φ$ are angular wave function. $R^{2}$ is known as radial probability density and $4 π r^{2} R^{2} d r$ is known as radial probability function i.e., the probability of finding the electron is spherical shell of thickness dr.
Number of radial node =n -l - 1
Number of angular node = l
For hydrogen atom, wave function for 1s and 2s-orbitals are:
$Ψ_{1 s} = \sqrt{\frac{1}{π a_{0}^{a}}} e_{r}^{- z_{r} / a_{0}}$
$Ψ_{2 s} = {(\frac{Z}{2 a_{0}})}^{½} (1 - \frac{Z r}{a_{0}}) e^{- \frac{Z r}{a_{0}}}$
The plot of radial probability function $4 π r^{2} R^{2}$ aganist r will be:

Answer the following questions:
The following graph is plotted for ns-orbitals

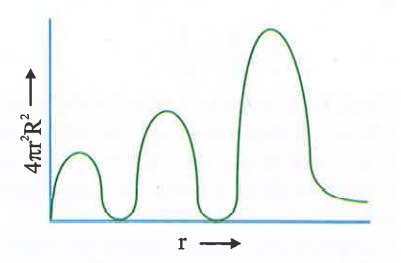
The value of 'n' will be:
A1
B2
C3
D4
Assertion. The plots of probability density and radial probability function versus distance r from the nucleus for any particular orbital are not identical
Reason. Probability density is $Ψ^{2}$ whereas radial probability function represents probability of finding the electron in a shell of thickness $d r$ .
AIf both assertion and reason are true, and reason is the true explanation of the assertion
BIf both assertion and reason are true, but reason is not the true explanation of the assertion
CIf assertion is true, but reason is false
DIf both assertion and reason are false
$ψ^{2}$ ,( psi) the wave function resperesents the probability of finding electron . Its value depends :
AHow much it is inside the nucleus
BHow much it is far from the the nuycleus
CHow much it is near the nucleus
DUpon the type of orbital

For s-orbitals, since ( $Ψ$ orbitals wave function) is independent of angles, the probability density $(Ψ^{2})$ is

The correct Answer is:C

( c) For spherical orbital
$Ψ = f (r) (r = distance from nucleus)$
Since $Ψ$ (orbital) is independent of angles therefore probability $(Ψ^{2})$ also independent of angles and spherically symmetric.

Topper's Solved these Questions

Similar Questions

Knowledge Check

$ψ^{2}$ ,( psi) the wave function resperesents the probability of finding electron . Its value depends :

A2Z-ATOMIC STRUCTURE-Quantum Numbers, Orbitial'S Shape, Electronic Configuration

For s-orbitals, since (Ψ orbitals wave function) is independent of angles, the probability density (Ψ2) is

The correct Answer is:C

( c) For spherical orbital Ψ=f(r)(r=distance from nucleus) Since Ψ (orbital) is independent of angles therefore probability (Ψ2) also independent of angles and spherically symmetric.

Topper's Solved these Questions

Similar Questions

Knowledge Check

ψ2 ,( psi) the wave function resperesents the probability of finding electron . Its value depends :

A2Z-ATOMIC STRUCTURE-Quantum Numbers, Orbitial'S Shape, Electronic Configuration

For s-orbitals, since ( $Ψ$ orbitals wave function) is independent of angles, the probability density $(Ψ^{2})$ is

( c) For spherical orbital
$Ψ = f (r) (r = distance from nucleus)$
Since $Ψ$ (orbital) is independent of angles therefore probability $(Ψ^{2})$ also independent of angles and spherically symmetric.

$ψ^{2}$ ,( psi) the wave function resperesents the probability of finding electron . Its value depends :