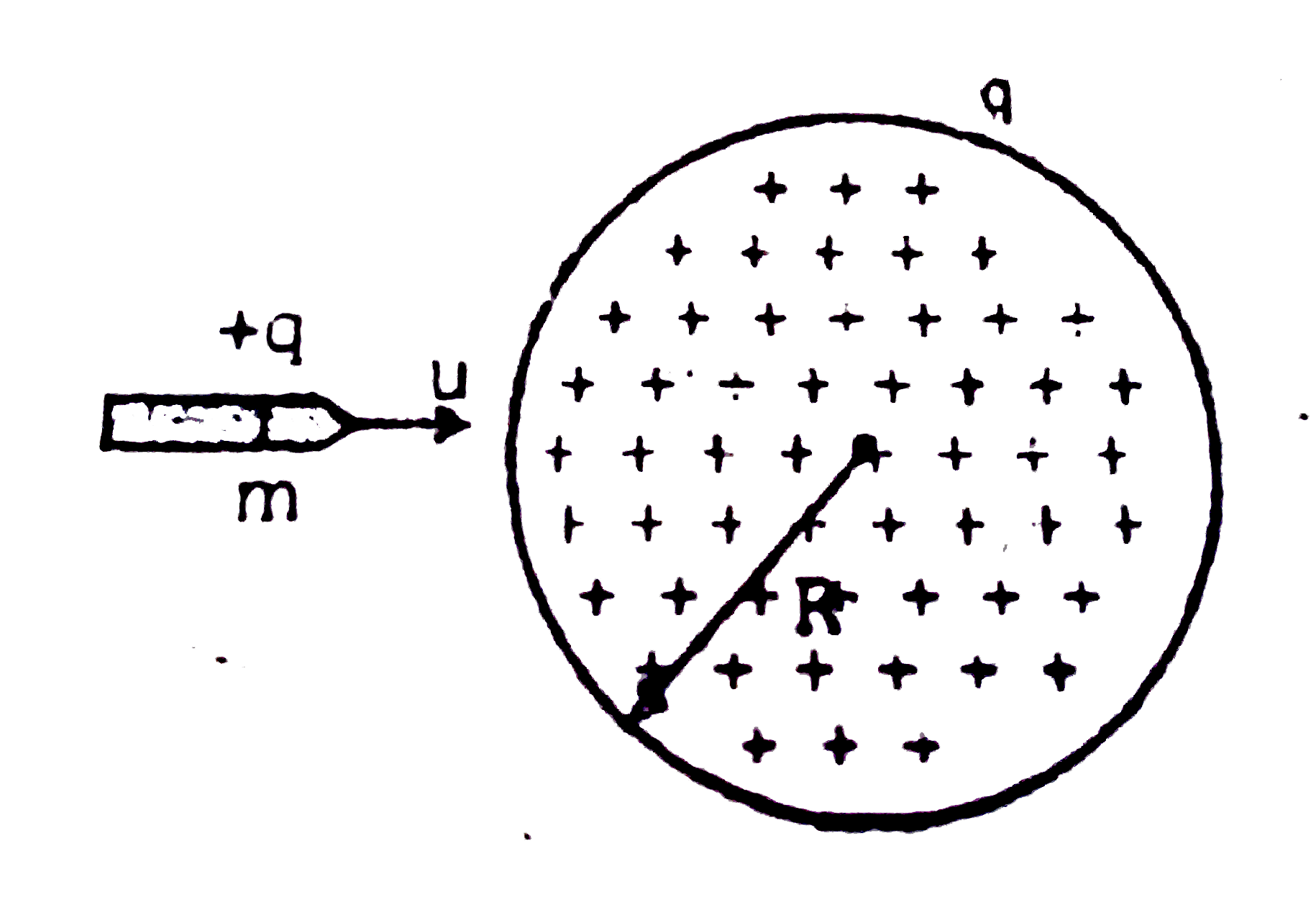
A particle of mass m and charge -q moves along a diameter of a uniform

A particle of mass m and charge -q moves diametrically through a uniformily charged sphere of radius R with total charge Q. The angular frequency of the particle's simple harminic motion, if its amplitude lt R, is given by
A $\sqrt{\frac{1}{4 π ε_{0}} \frac{q Q}{m R}}$
B $\sqrt{\frac{1}{4 π ε_{0}} \frac{q Q}{m R^{2}}}$
C $\sqrt{\frac{1}{4 π ε_{0}} \frac{q Q}{m R^{3}}}$
D $\sqrt{\frac{1}{4 π ε_{0}} \frac{m}{q Q}}$
A bullet of mass m and charge q is fired towards a solid uniformly charge sphere of radius R and total charge +q. If it strikes the surface of sphere with speed u, find the minimum value of u so that it can penetrate through the sphere. (Neglect all resistance force or friction acting on bullet except electrostatic forces)

A $\frac{q}{\sqrt{2 π ε_{0} m R}}$
B $\frac{q}{\sqrt{4 π ε_{0} m R}}$
C $\frac{q}{\sqrt{8 π ε_{0} m R}}$
D $\frac{\sqrt{3} q}{\sqrt{4 π ε_{0} m R}}$
A particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
AAways circular
Bcircular, If $v \times B = 0$
Ccircular,If $v . B = 0$
DNone of these

A particle of mass m and charge -q moves along a diameter of a uniformluy charged sphere of radinus $R$ and carrying a total charge $+ Q$ . Find the frequency of S.H.M. of the particle if the amplitude does not exceed .