The plates of parallel capaitor are given charges +4Q and −2Q. The capacitor is then connected across an uncharged capacitor of same capacitances first one (=C). Find the final potential difference between the plates of the first capacitor.
The correct Answer is:3Q/2C
To solve the problem, we need to find the final potential difference between the plates of the first capacitor after it is connected to an uncharged capacitor of the same capacitance. Let's break this down step by step.
Step 1: Understand the Initial Charges
The first capacitor has charges of +4Q and -2Q on its plates.
Step 2: Calculate the Initial Charge on the Capacitor
The net charge on the first capacitor can be calculated as follows:
- The charge on one plate is +4Q.
- The charge on the other plate is -2Q.
- The effective charge (Q_eff) is given by:
Qeff=+4Q−2Q=+2Q
Step 3: Determine the Charge Distribution
When the first capacitor is connected to the uncharged capacitor, charge will redistribute between the two capacitors. The total charge before connection is +2Q.
Step 4: Calculate the Final Charges
Let Q′1 and Q′2 be the final charges on the plates of the first capacitor after connection, and since the second capacitor is uncharged initially, it will take some charge from the first capacitor.
Using charge conservation:
Q′1+Q′2=2Q
Since the second capacitor is uncharged, it will take a portion of the charge from the first capacitor.
Step 5: Set Up the Equations
Let the final potential difference across the first capacitor be V. The charge on the first capacitor can be expressed as:
Q′1=C⋅V
For the second capacitor, which is also of capacitance C, the charge will be:
Q′2=C⋅V2
Since the second capacitor starts with 0 charge, we can assume:
Q′2=−Q′1+2Q
Step 6: Solve for the Final Potential
From the charge conservation equation:
Q′1+Q′2=2Q
Substituting Q′2:
Q′1−Q′1+2Q=2Q
This means:
Q′1=3Q/2
Step 7: Calculate the Final Potential Difference
Now, substituting back to find the potential difference:
V=Q′1C=3Q/2C=3Q2C
Final Answer
The final potential difference between the plates of the first capacitor is:
V=3Q2C
The first capacitor has charges of +4Q and -2Q on its plates.
The net charge on the first capacitor can be calculated as follows:
- The charge on one plate is +4Q.
- The charge on the other plate is -2Q.
- The effective charge (Q_eff) is given by:
Qeff=+4Q−2Q=+2Q
When the first capacitor is connected to the uncharged capacitor, charge will redistribute between the two capacitors. The total charge before connection is +2Q.
Let Q′1 and Q′2 be the final charges on the plates of the first capacitor after connection, and since the second capacitor is uncharged initially, it will take some charge from the first capacitor.
Q′1+Q′2=2Q
Since the second capacitor is uncharged, it will take a portion of the charge from the first capacitor.
Let the final potential difference across the first capacitor be V. The charge on the first capacitor can be expressed as:
Q′1=C⋅V
For the second capacitor, which is also of capacitance C, the charge will be:
Q′2=C⋅V2
Since the second capacitor starts with 0 charge, we can assume:
Q′2=−Q′1+2Q
From the charge conservation equation:
Q′1+Q′2=2Q
Substituting Q′2:
Q′1−Q′1+2Q=2Q
This means:
Q′1=3Q/2
Now, substituting back to find the potential difference:
V=Q′1C=3Q/2C=3Q2C
The final potential difference between the plates of the first capacitor is:
V=3Q2C
Similar Questions
Knowledge Check
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1In a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
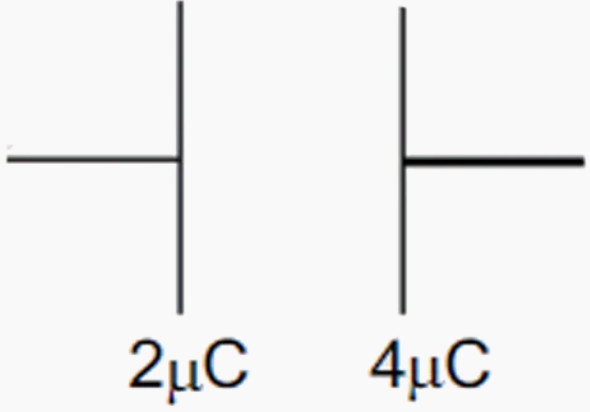 A2 voltB1 voltC4 voltD3 volt
A2 voltB1 voltC4 voltD3 voltConsider a parallel plate capacitor originally with a charge q0 capacitance C0 and potential difference ΔV0 There is an electrostatic force of magnitude F0 between the plates and the capacitor has a stored energy U0. The terminals of the capacitor are connected to another capacitor of same capacitance and charge.
A dielectric slab with ke>1 is inserted between the plates of the first capacitor . Which quantity decreases?AqBCCΔVDF
Two parallel conducting plates of a capacitor of capacitance C containing charges Q and -2Q at a distance d apart. Find out potential difference between the plates of capacitors.
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V. It is then connected to another uncharged capacitor having the same capacitance. Find out the ratio of the energy stored in the combined system to that stored initially in the single capacitor.
View SolutionIn an isolated parallel plate capacitor of capacitance C, the plates have charge Q1 and Q2. The potential difference between the plates is
View SolutionThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View SolutionA capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
View Solution