A long thin walled pipe of radius R carries a current I along its length The current density is uniform over the circumference of the pipe The magnetic field at the center of the pipe due to quarter portion of the pipe shown, is
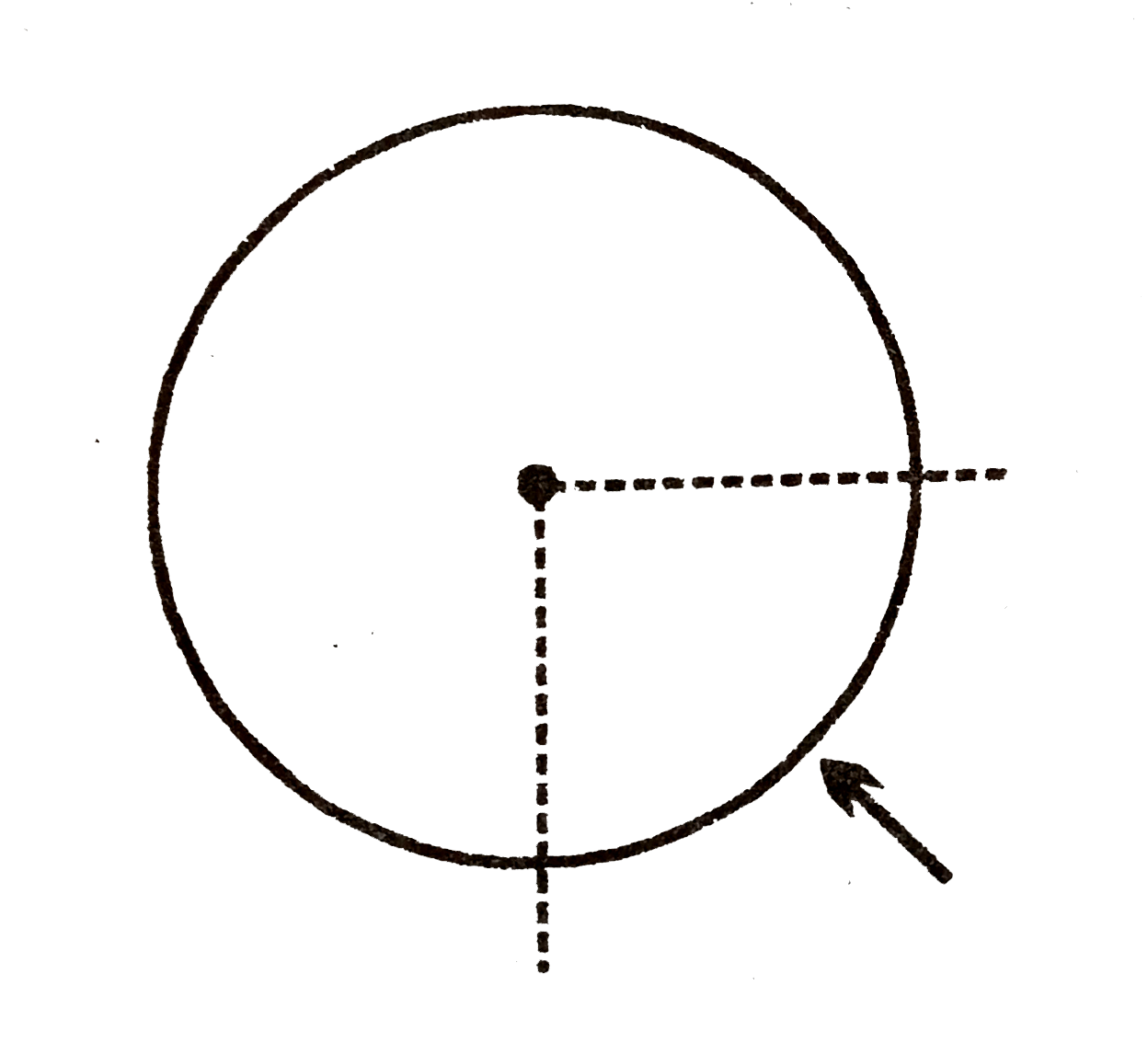 .
.
μ0I√24π2R
μ0Iπ2R
2μ0I√2π2R
None
The correct Answer is:A
dI=I2πdthη
Field at center due to very long wire carrying current dI
dB=μ02π=IR=μ04π2IRdthη
→B=∫d→B=⎡⎢
⎢⎣π/2∫0dBcosθˆi+π/20i∫0dBsinθˆi⎤⎥
⎥⎦
=μ04π2RIR⎡⎢
⎢⎣π/2∫0cos0dthηˆi+π/20i∫0sin0dθˆj⎤⎥
⎥⎦
→B=μ04π2RIR[ˆi+ˆj]⇒B=μ04π2RIR√2
 .
.
Similar Questions
Knowledge Check
A circular coil of n turns and radius r carries a current I. The magnetic field at the center is
Aμ0nIrBμ0nI2rC2μ0nIrDμ0nI4rA direct current l flow along the length of an infinitely long striaght thin walled pipe then the magnetic field is
Auniform throughout the pipe but not zeroBzero only along the axis of the pipeCzero at any point inside the pipeDmaximum at the center and minimum at the edgeA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
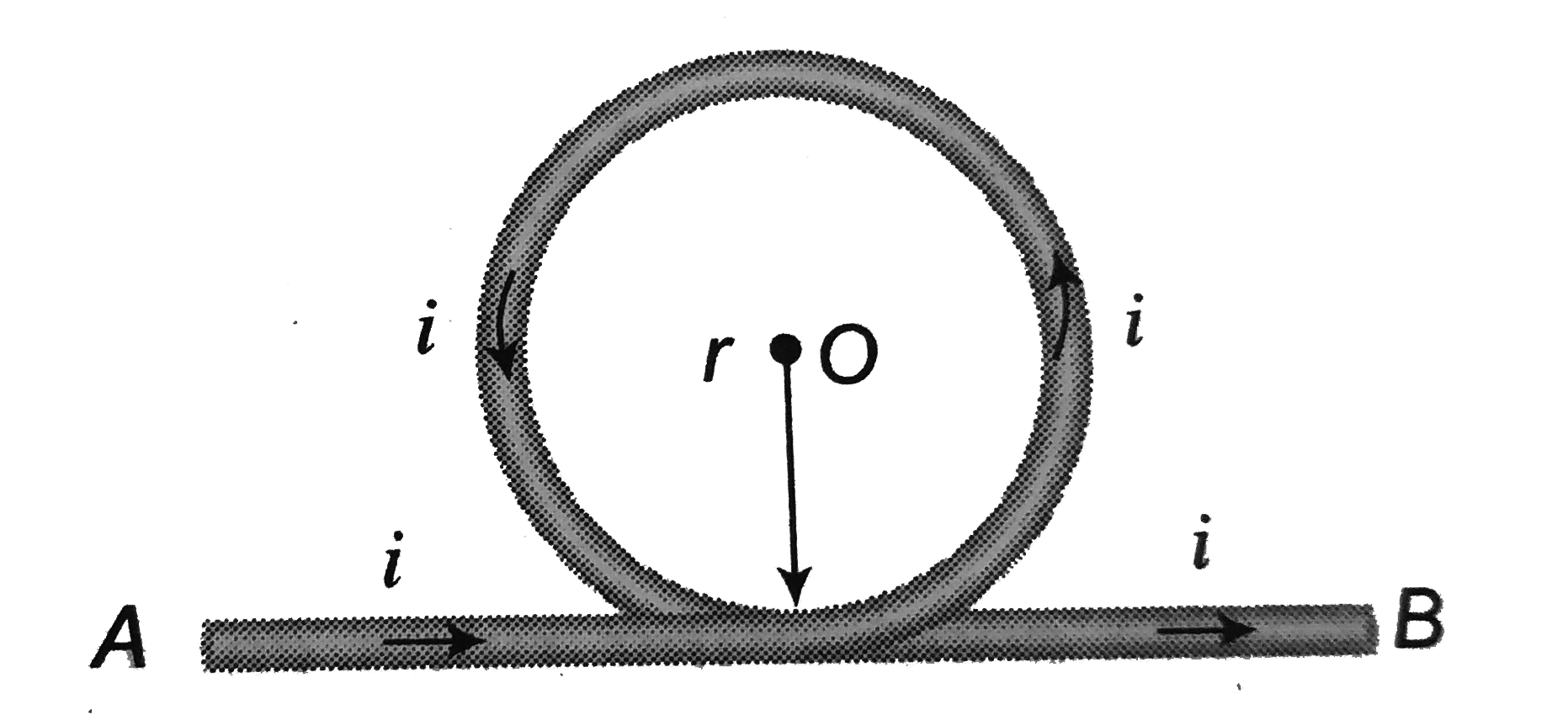 Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)
Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)
A thin but long, hollow, cylindrical tube of radius r carries a current i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
View SolutionA long cylinder of uniform cross section and radius R is carrying a current i along its length and current density is uniform cross section and radius r in the cylinder parallel to its length. The axis of the cylinderical cavity is separated by a distance d from the axis of the cylinder. Find the magnetic field at the axis of cylinder.
View SolutionFind the magnitude of the magnetic field at the origin O due to very long conductor carrying current I of the shape as shown in figure.
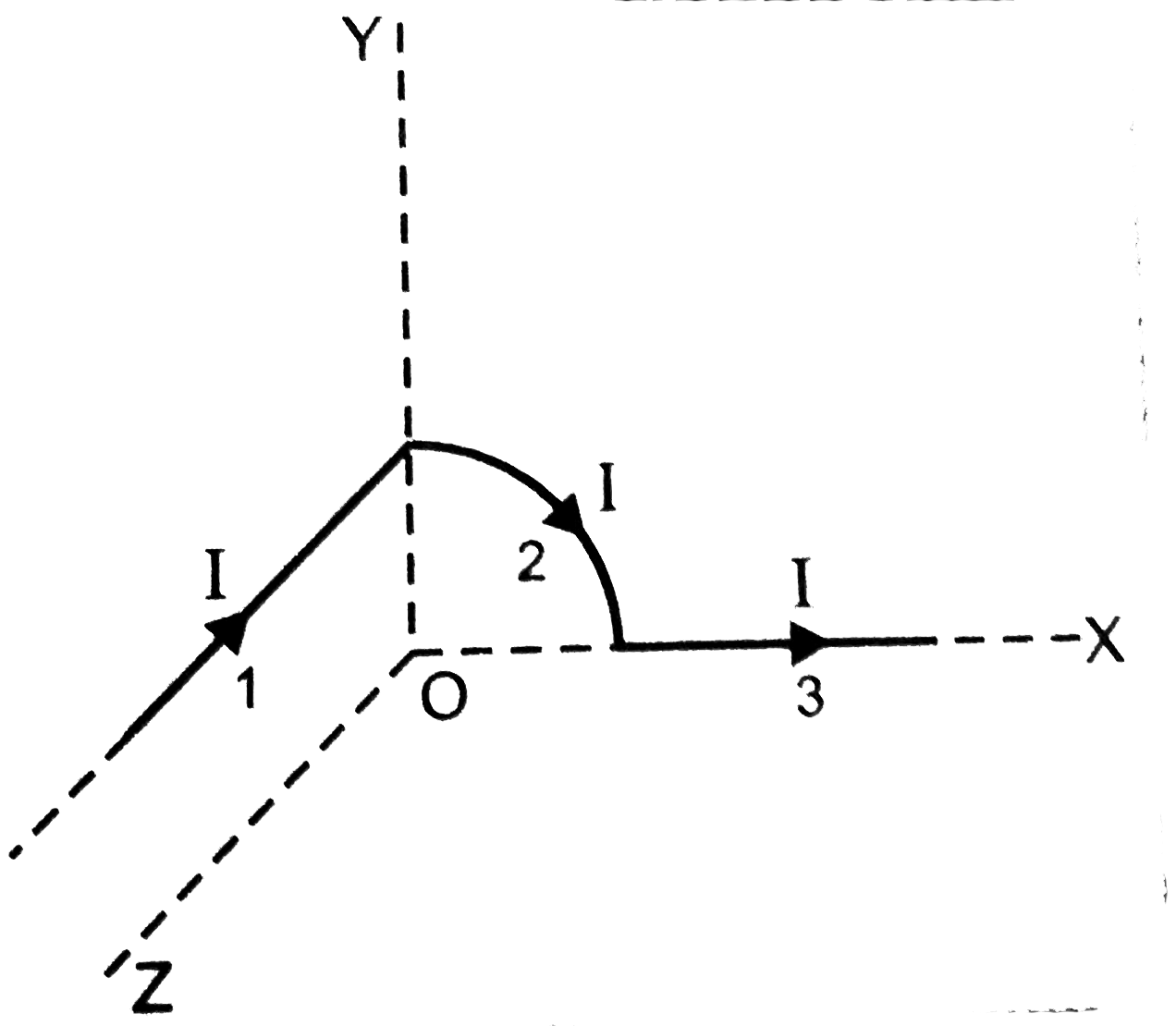
View SolutionConsider the loop PQRSP, carrying clockwise current i, shown in the figure. The magnitude of magnetic field at the centre O of the curved portion is
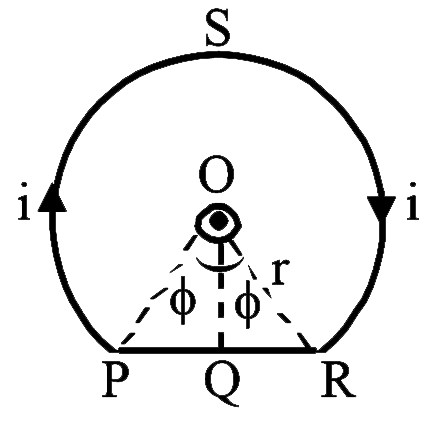
View SolutionA direct current / flows along the length of an infinitely long straight thin walled pipe, then the magnetic field is
View Solution
