Two particles of charges $+ Q$ and $- Q$ are projected from the same point with a velocity v in a region of unifrom magnetic filed $B$ such that the velocity vector makes an angle 0 with the magnetic filed Their masses are $M$ and $2 M$ respectively Then, they will meet again for the first time at a point whose distane from the point of projection is .

A

$2 π M v cos 0 / q B$

B

$8 π M v cos 0 / q B$

C

$π M v cos 0 / q B$

D

$4 π M v cos 0 / q B$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$T_{1} = \frac{2 π M}{q B} T_{2} = \frac{2 π (2 M)}{q B} \Rightarrow T_{2} = \frac{4 π M}{q B}$
they will meet again when first will complete two revolution and second will complete one revoluation so direction
$d = v cos θ t = v cos θ .2 \frac{2 π M}{q B} = \frac{4 π M v cos θ}{q B}$ .

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Similar Questions

Knowledge Check

Question 1 - Select One
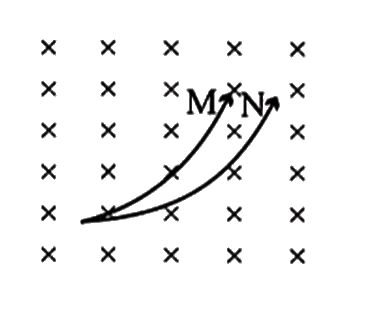
Two particles $A$ and $B$ are projected from the same point in different direction in such a manner that their velocity vectors are shown in the diagram $: -$
.
A $T_{A} = T_{B}$
B $T_{A} > T_{B}$
C $T_{A} < T_{B}$
DCan't be determined
Question 2 - Select One
A particle of charge $q$ is projected from point $P$ with velocity $v$ as shown. Choose the correct statement from the following.

AMagnetic field at $P$ is $\frac{μ_{0} i}{4 π r} [2 + \sqrt{2}] ⊙$
BThe magnetic field at $P$ is $μ_{0} i / 2 π r .$
CThe particle initially accelerated towards wire $A$ .
DThe particle initially accelerated towards wire $B$ .
Question 3 - Select One
A particle of specific charge $q / m = (π) C / k g$ is projected from the origin towards positive x-axis with a velocity of $10 m / s$ in a uniform magnetic field $\to B = - 2 ˆ K$ Tesla. The velocity $\to V$ of the particle after time $t = 1 / 6$ s will be
A $(5 ˆ i + 5 \sqrt{3} ˆ j) m / s$
B $10 ˆ j m / s$
C $(5 \sqrt{3} ˆ i + 5 ˆ j) m / s$
D $- 10 ˆ j m / s$

Recommended Questions

Home
Ask Doubt
Profile