Side rail of length 2L are fixed on a horizontalplane at a distane l from each other These ends aer connected by two identical ideal batteries with emf E by sistancelesss wires (see) On therails is a rod of mass m, which may slide along them The entire system is placed in a uniform vertical magnetic field B Assuming that the resistance of the rodi is R and the resistance per unit length of each of therails equal to p find the period of small oscillations (in sec) arsing from shifting therod from the equlibrium along the rails Neglect friction internal resistance of batteries and induced emf in the rod [Take:B=πT,ɛ=πvo<l=0.5,L=1m,p=1Ω/m,R=0.25Ωm=100gm] .
![Side rail of length 2L are fixed on a horizontalplane at a distane l from each other These ends aer connected by two identical ideal batteries with emf E by sistancelesss wires (see) On therails is a rod of mass m, which may slide along them The entire system is placed in a uniform vertical magnetic field B Assuming that the resistance of the rodi is R and the resistance per unit length of each of therails equal to p find the period of small oscillations (in sec) arsing from shifting therod from the equlibrium along the rails Neglect friction internal resistance of batteries and induced emf in the rod [Take : B = pi T, varepsilon = pi volt l = 0.5, L =1m,p = 1Omega//m,R =0.25Omega m = 100 gm] .](https://d10lpgp6xz60nq.cloudfront.net/physics_images/NG_PHY_C04_E01_103_Q01.png)
The correct Answer is:0001
Similar Questions
A glass rod of length l moves with velocity in a uniform magnetic field B. What is the e.m.f. induced in the rod ?
View SolutionShows a rod of length l and resistance r moving on two rails shorted by a resistance R. A uniform magnetic field B is present normal to the plane of rod and rails. Show the electrical equivalence of each branch.
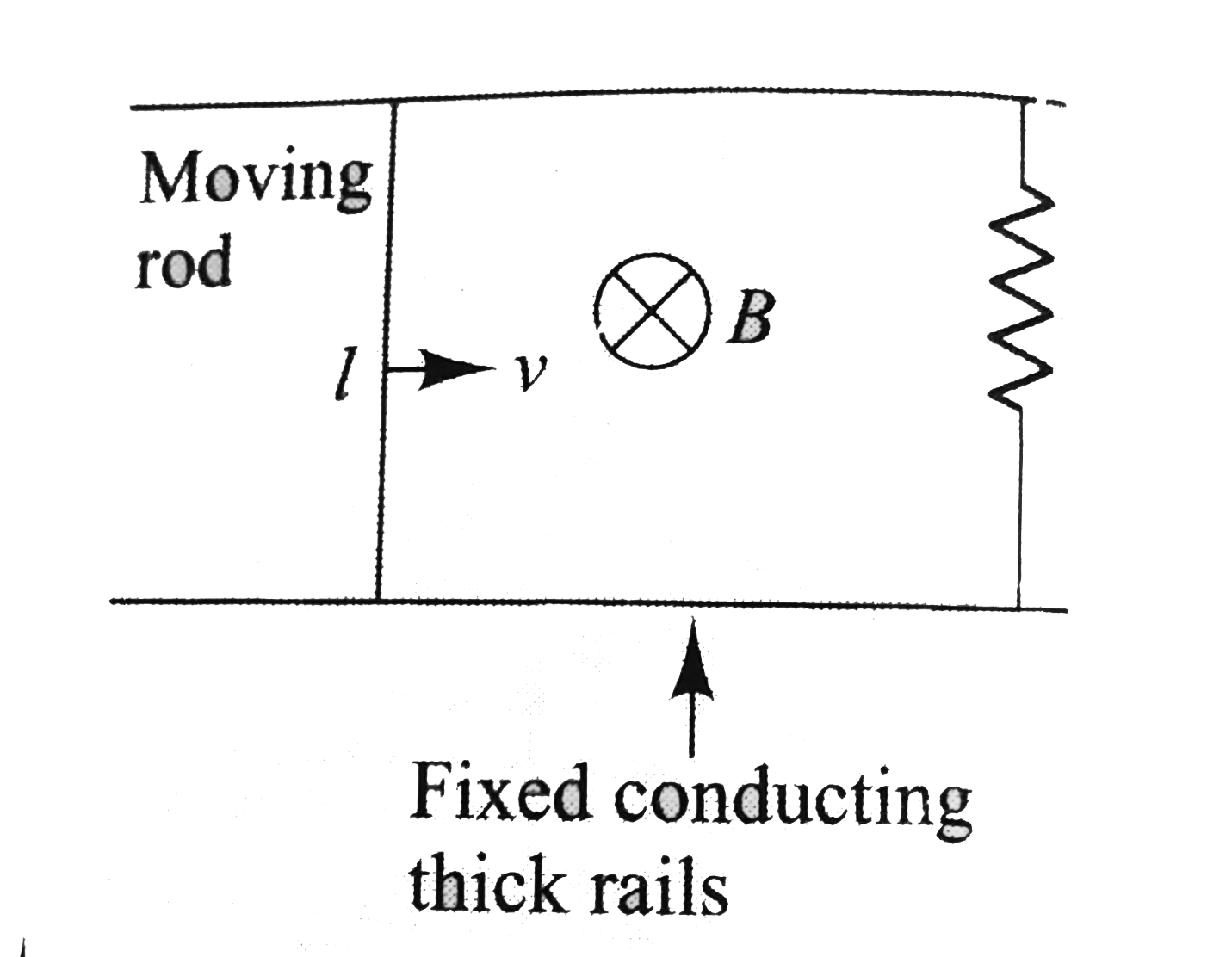
View Solution
Knowledge Check
A rod of mass M and length l is suspended by two wires P and Q. A uniform magnetic field 'B' is directed into the page. When current through the rod is l. Then the tension in each supporting wire is-
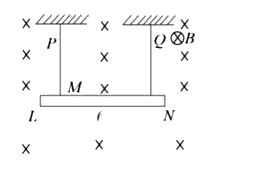 Amg2B2BIlCMg−BilDMg−Bil2
Amg2B2BIlCMg−BilDMg−Bil2An inductance L and a resistance R are connected in series with a battery of emf ε. The maximum rate at which the energy is stored in the magnetic field is :
Aε4RBε2RC2RεD4RεAn inductance L and a resistance R are connected in series with a battery of emf ε. The maximum rate at which the energy is stored in the magnetic field is :
Aε4RBε2RC2RεD4Rε
Shows a rod of length l and resistance r moving on two rails shorted by a resistance R. A uniform magnetic field B is present normal to the plane of rod and rails. Show the electrical equivalence of each branch.
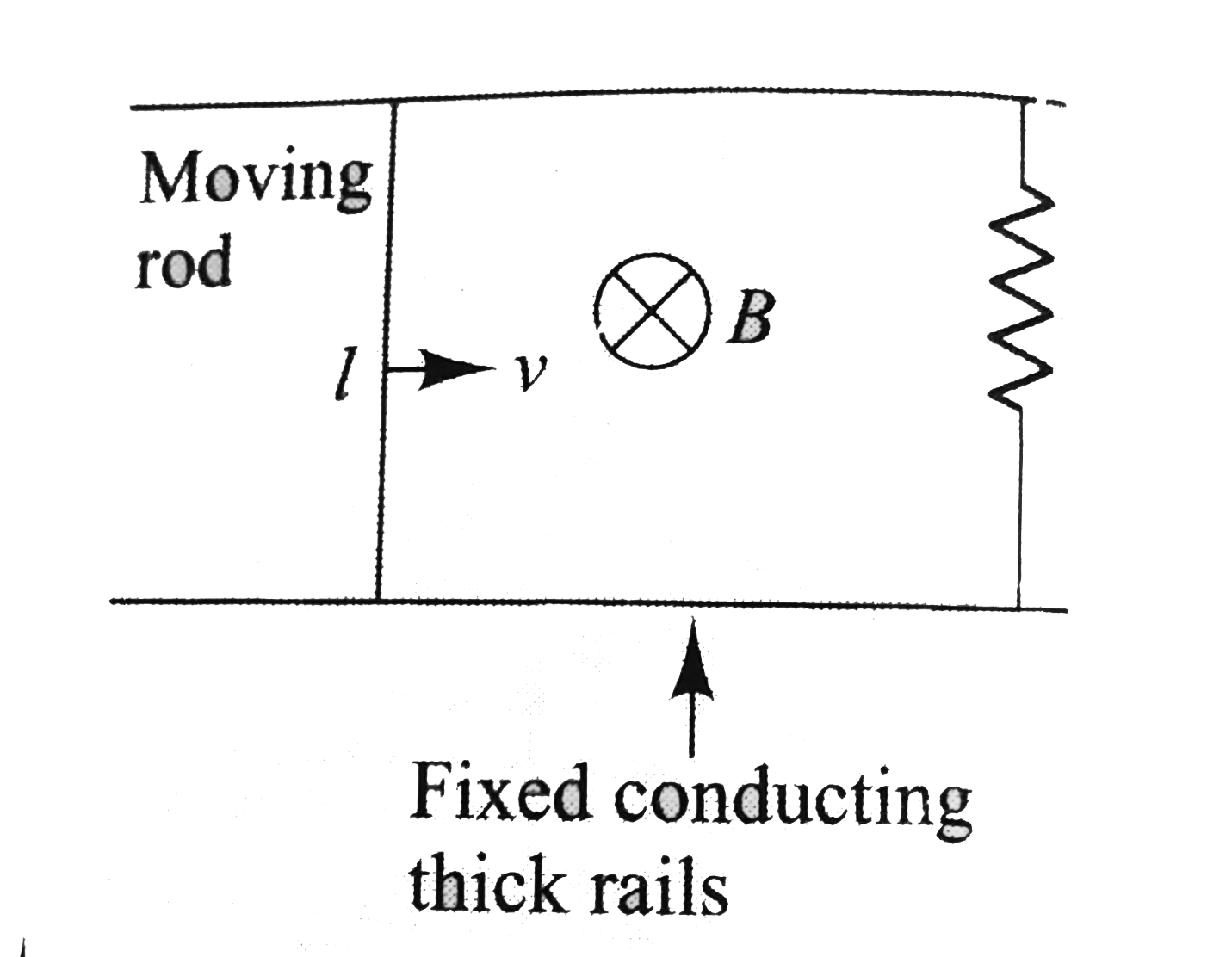
View SolutionShows a rod of length l and resistance r moving on two rails shorted by a resistance R. A uniform magnetic field B is present normal to the plane of rod and rails. Show the electrical equivalence of each branch.
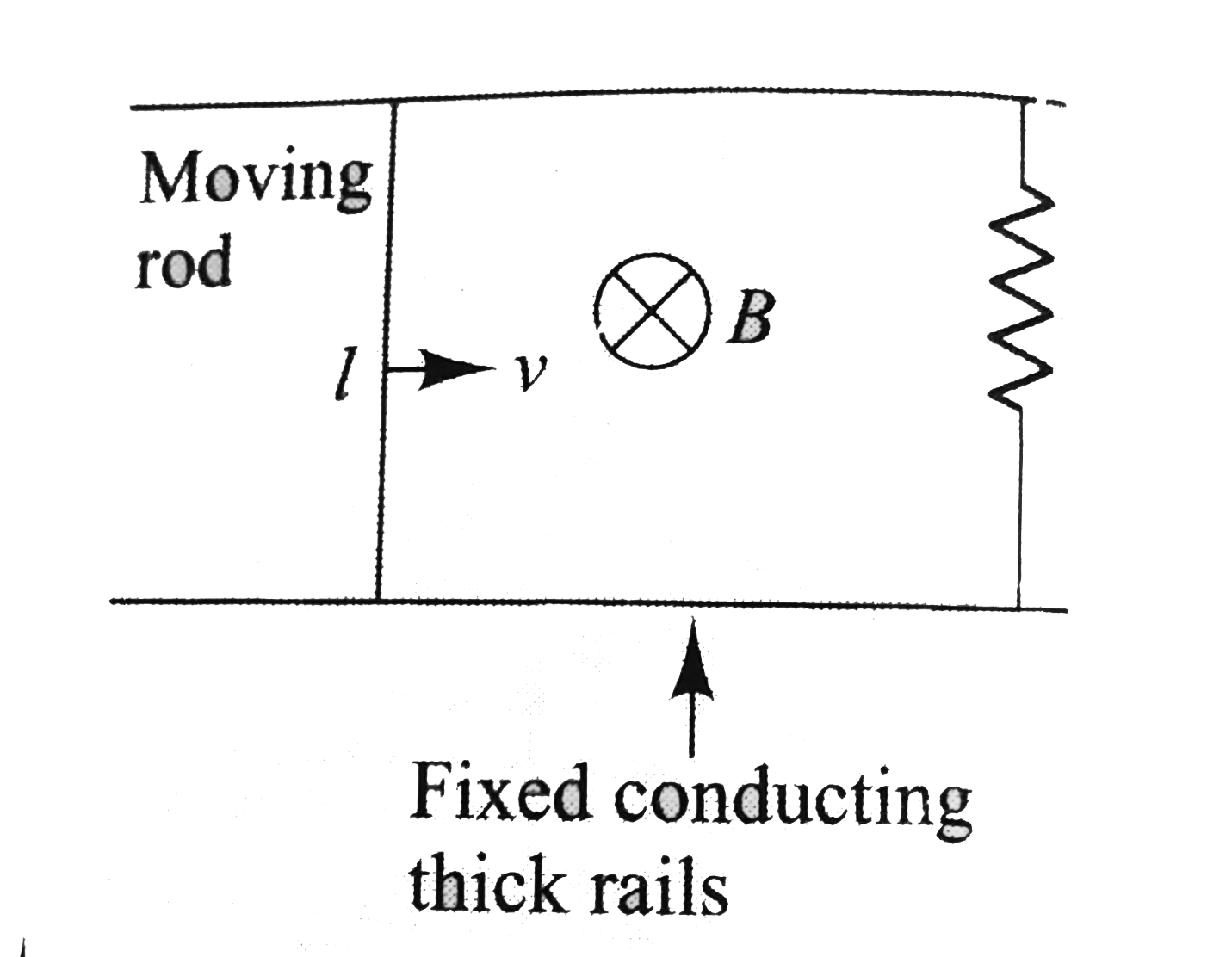
View SolutionA wire of mass m and length I can freely slide on a pair of parallel, smooth, horizontal rails placed in a vertical magnetic field B . The rails are connected by a capacitor of capacitance C. The electric resistance of the rails and the wire is zero. If a constant force F acts on the wire as shown in the figure, find the acceleration of the wire.
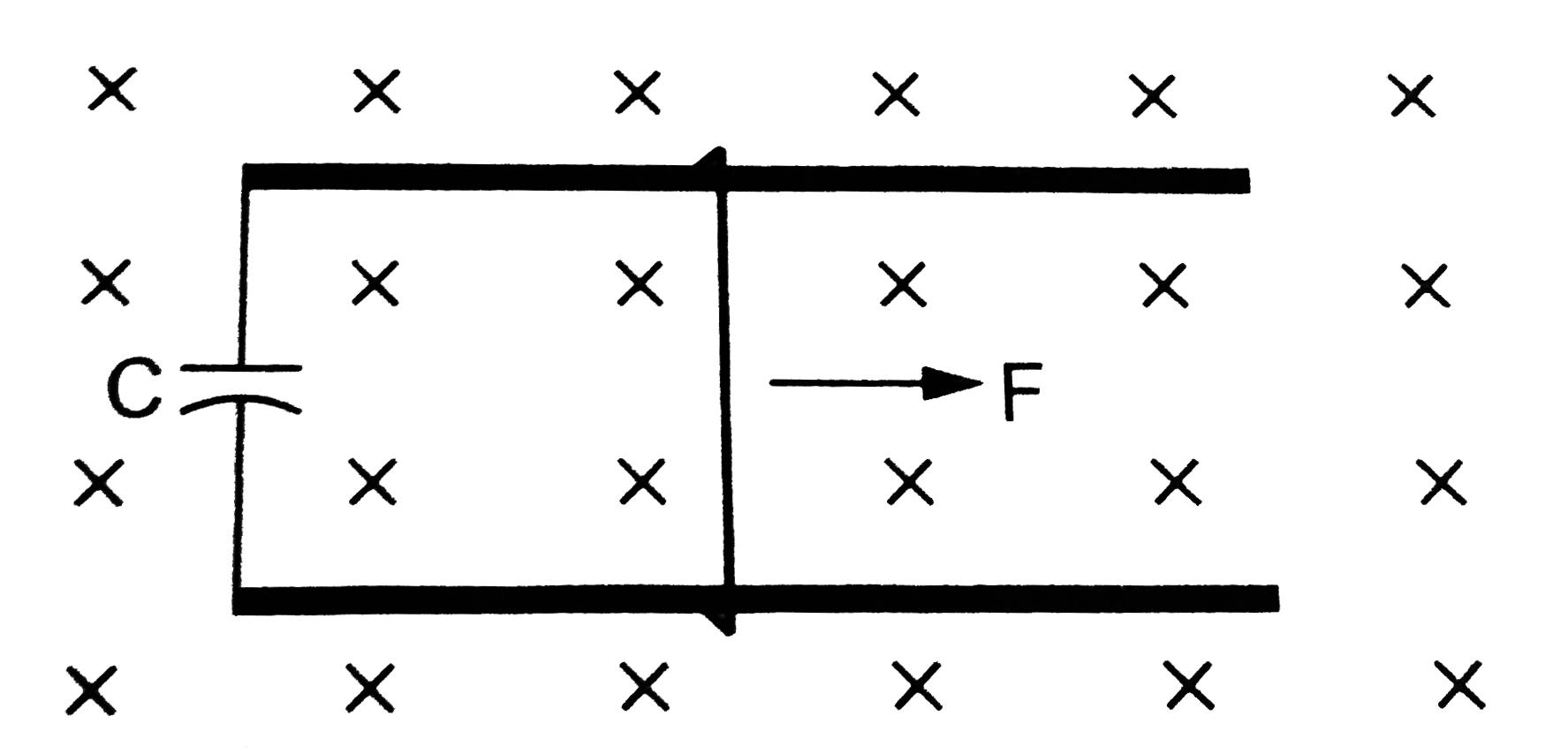
View SolutionThe current generator ig, shown in , sends a constant current I through the circuit. The wire ab has a length l and mass m and can slide on the smooth, horizontal rails connected to lg. The entire system lies in a vertical magnetic field B. Find velocity of the wire as a function of time.

View SolutionA wire having mass m and length 1 can freely slide on a pair or parallel smooth horizontal rails placed in vertical magnetic field B. The rails are connected by a capacitor of capacitance C . The electric resistance of the rails and the wire is zero .If a constant force F acts on the Wire as shown in the figure . Then ,the acceleration of the wire can be given as

View Solution
