The velocity of any particle is related with its displacement As, x=√v+1, Calculate acceleration at x=5m.
x=√v+1⇒x2=v+1⇒v=(x2−1)
Therefore
a=dvdt=ddt(x2−1)=2xdxdt=2xv=2x(x2−1)
at x=5ma=2×5(25−1)=240m/s2
Similar Questions
Knowledge Check
The velocity of a particle varies with its displacement as v=(√9−x2)ms−1.
Find the magnitude of the maximum acceleration of the particle.A3ms−2B4ms−2C3.5ms−2D5ms−2If the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
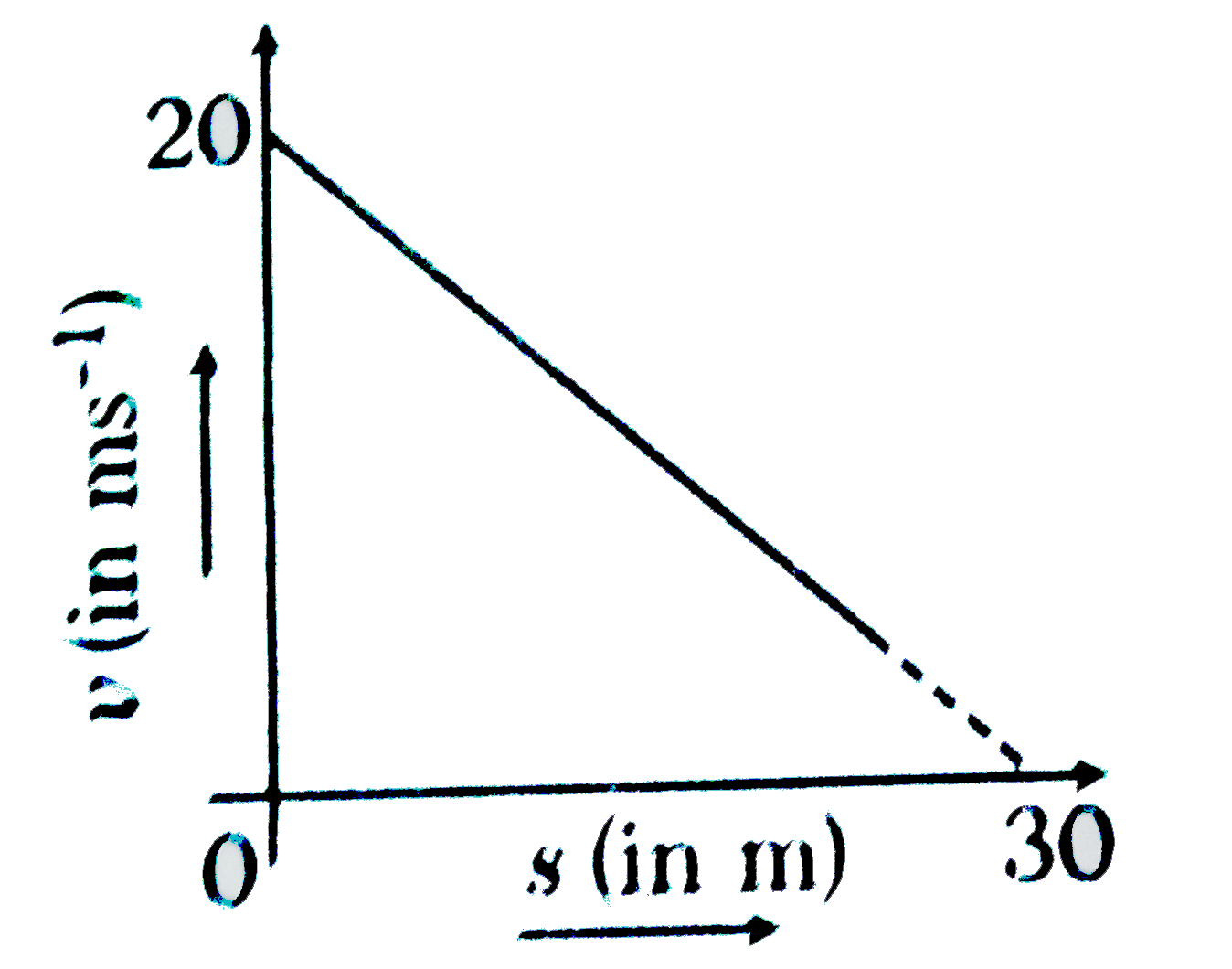 A23ms−2B−23ms−2C203ms−2D−203ms−2
A23ms−2B−23ms−2C203ms−2D−203ms−2
If the velocity of a body related to displacement x is given by v=√5000+24x m/s, then the acceleration of the body is _______m/s2.
View SolutionThe velocity v of moving object varies with displacement u as v=3x^(2)-2 ,then the acceleration at x=2m is
View SolutionIf v=√5000+24xms then calculate acceleration.
View SolutionVelocity of a particle moving in a straight line varies with its displacement as v=√4+4xm/s where x is displacement. Displacement of particle at time t = 0 is x = 0. Find displacement (in m) of particle in 2 sec.
View SolutionThe velocity of particle is given by v=√gx . Find its acceleration.
View SolutionThe velocity time relation of a particle is given by v =(3t2−2t−1)m/s Calculate the position and acceleration of the particle when velocity of the particle is zero . Given the initial position of the particle is 5m .
View Solution
