At aharbour enemy ship is at a distance $180 \sqrt{3} m$ form the security cannot having a muzzle velocity of $60 m / s$ .
(a) To what angle must the cannot be elevated to hit the ship.
(b) What is the time of flight.
(c ) How for should the ship be moved away from its initial position so that it becomes beyond the range of the cannot $(g = 10 m / s^{2})$ .

Video Solution

Text Solution

Verified by Experts

(a) For hitting the ship the range of cannon must be equal to the distance of ship from cannot i.e.,
Range $= 180 \sqrt{3}$

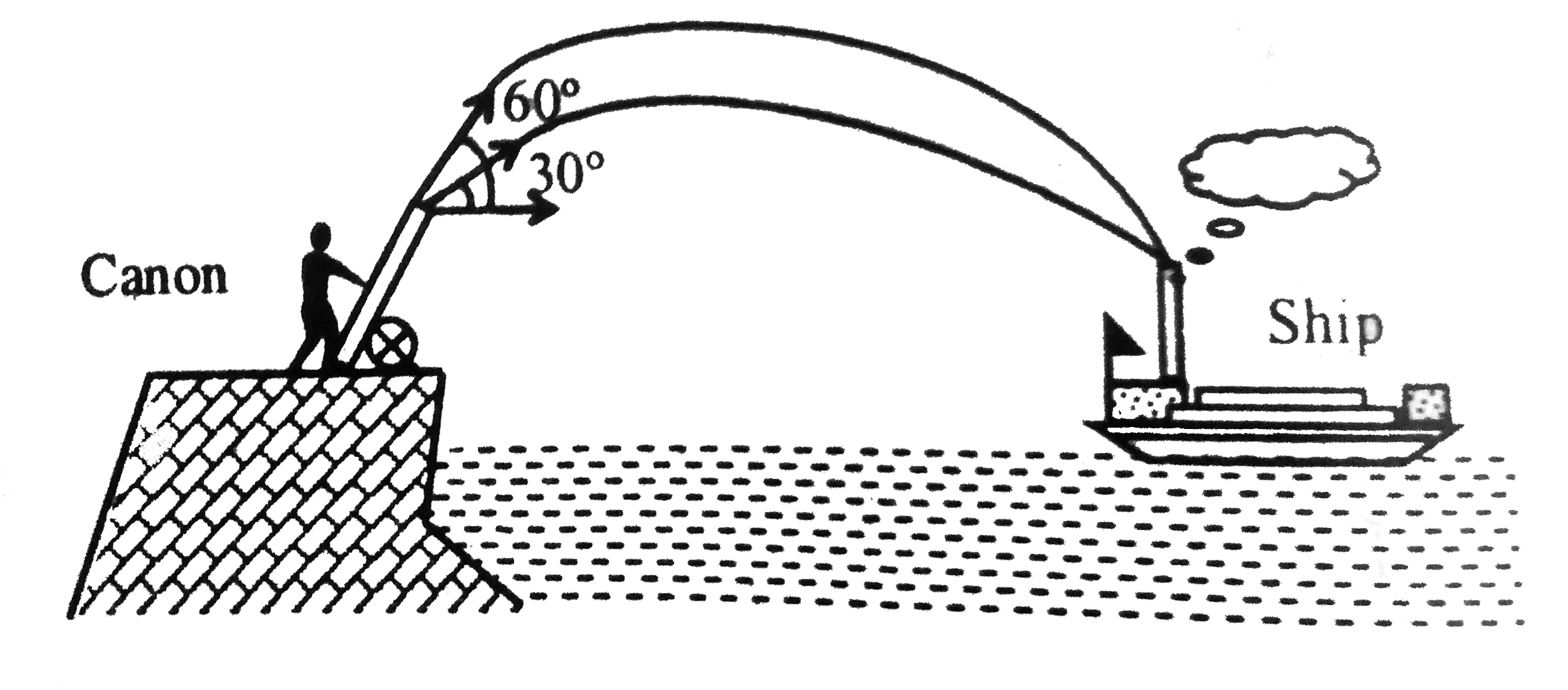
$\frac{u^{2} sin 2 θ}{g} = 180 \sqrt{3}$
r $sin 2 θ = \frac{180 \sqrt{3} \times 10}{60 \times 60} = \frac{\sqrt{3}}{2}$
$\begin{matrix} i . e . & 2 θ = 60^{\circ} & or & 120^{\circ} or & θ = 30^{\circ} & or & 60^{\circ} \end{matrix}$
(a) The cannot mist be elevated at an angle of $30^{\circ}$ or $60^{\circ}$
(b) As $T = (2 u sin θ / g)$ , depending on $θ$ there are two times of flight which are given by
$t_{1} = \frac{2 \times 60}{10} \times sin 30 = 6 s$
and $t_{2} = \frac{2 \times 60}{10} \times sin 60 = 6 \sqrt{3} = 104 s$ .
(c) The maximum range of cannot (where $θ = 45^{\circ})$
$R_{max} = \frac{u^{2}}{g} = \frac{60 \times 60}{10} = 360 m$
And as initially the ship is $180 \sqrt{3} m$ , so to become out of maximum range of cannot, the ship should be moved away form the harbour form its initial position by at least
$360 - 180 \sqrt{3} = 48.6 m .$

Updated on:21/07/2023

A particle $A$ is projected from the ground with an initial velocity of $10 m / s$ at an angle of $60^{\circ}$ with horizontal. From what height should an another particle $B$ be projected horizontally with velocity $5 m / s$ so that both the particles collide in ground at point $C$ if both are projected simultaneously $g = 10 m / s^{2}$ .

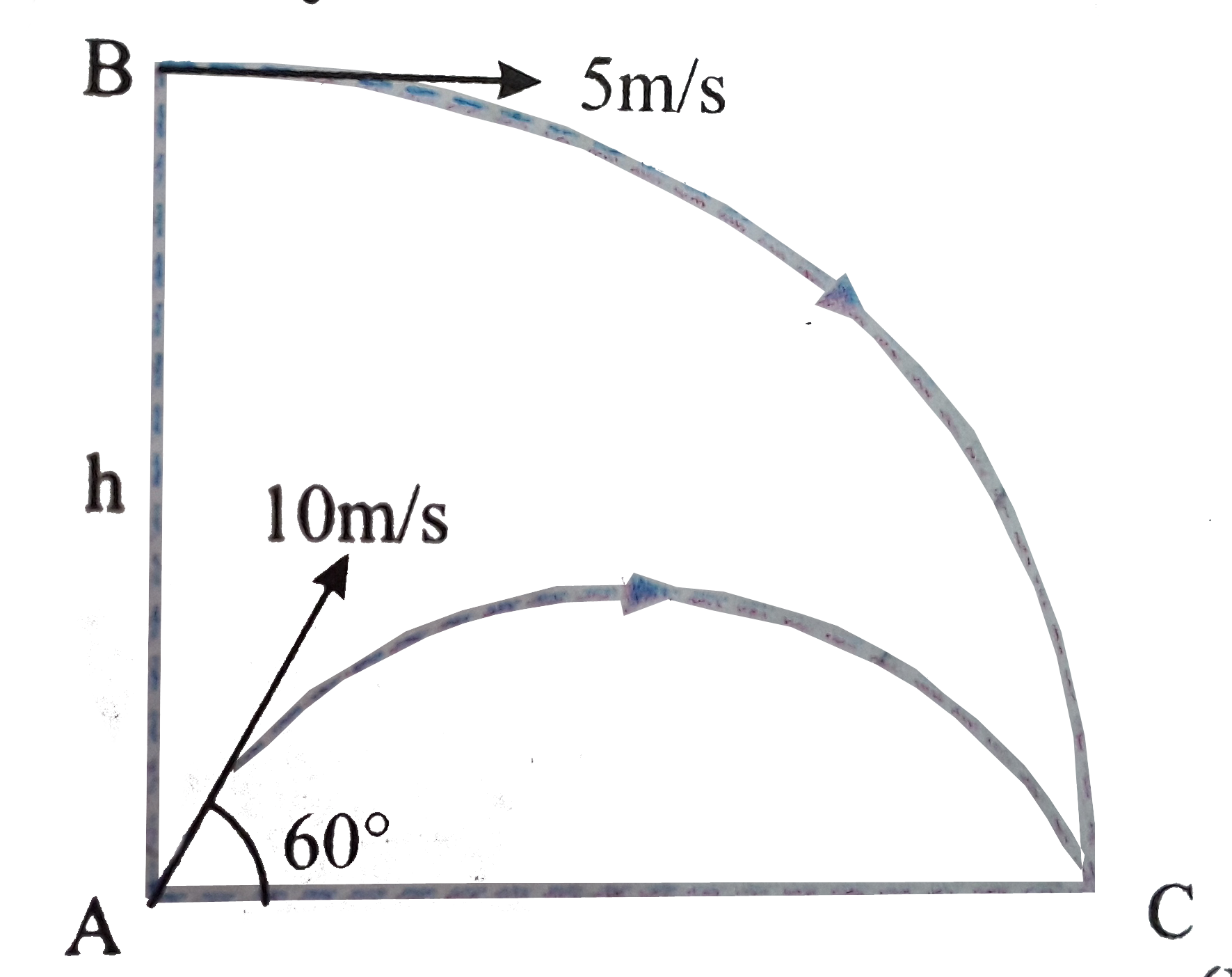A $10 m$
B $15 m$
C $20 m$
D $30 m$
Velocity $v$ of a particle moving along x axis as a function of time is given by $v = 2 t m / s$ . Initially the particle is to the right of the origin and $2 m$ away from it. Find the position (distance from origin) of the particle after first $3 s$ .

A5 m
B7 m
C11 m
D9 m
At what height above the ground must a mass of 5 kg be to have its PE equal in value to the KE possessed by it when it moves with a velocity of 10 m/s? $(g = 10 \frac{m}{s^{2}})$
A $1 m$
B $5 m$
C $10 m$
D $50 m$