Two projectiles are thrown simultaneously in the same plane from the same point. If their velocities are v1 and v2 at angles θ1 and θ2 respectively from the horizontal, then ansewer the following questions
If v1cosθ1=v2cosθ2, then choose the incrorrect statement
one particle will remain exactly below or above the other particle
the trajectory of one with respect to other will be a vertical straight line
both will have the same range
none of these
The correct Answer is:C
To solve the problem, we need to analyze the given conditions and the statements provided about the two projectiles.
Given:
- Two projectiles are thrown simultaneously from the same point.
- Their velocities are v1 and v2 at angles θ1 and θ2 respectively.
- It is given that v1cosθ1=v2cosθ2.
Objective:
Identify the incorrect statement based on the given conditions.
1. Understanding the Horizontal Components:
The condition v1cosθ1=v2cosθ2 indicates that the horizontal components of the velocities of both projectiles are equal. This means both projectiles will have the same horizontal displacement over time.
Hint: Remember that the horizontal component of velocity affects how far the projectile travels horizontally.
2. Analyzing the Vertical Motion:
The vertical components of the velocities are given by v1y=v1sinθ1 and v2y=v2sinθ2. The time of flight for each projectile can be calculated using the vertical motion equations, which depend on the vertical components of their velocities.
Hint: The time of flight is influenced by the vertical component of the velocity and the acceleration due to gravity.
3. Time of Flight Comparison:
Since the horizontal components are equal, we can conclude that if the time of flight is the same, the horizontal distance covered will also be the same. However, the time of flight may not necessarily be the same unless the vertical components are also equal.
Hint: Check if the vertical components lead to the same time of flight.
4. Maximum Height:
The maximum height attained by each projectile can be calculated using the vertical components. If the vertical components are equal, then the maximum heights will also be equal.
Hint: Maximum height depends on the vertical component of the initial velocity.
5. Trajectory with Respect to Each Other:
Since the horizontal components are equal, the trajectory of one projectile with respect to the other will appear as a vertical straight line when viewed from the frame of reference of one of the projectiles.
Hint: Think about how the relative motion looks when two objects have the same horizontal speed.
6. Identifying the Incorrect Statement:
The statements can be analyzed:
- If the horizontal components are equal, the trajectories will be vertical lines.
- The time of flight is not guaranteed to be the same unless the vertical components are also equal.
- The maximum heights can be equal if the vertical components are equal.
The incorrect statement is likely to be one that assumes equal ranges or equal times of flight without confirming the vertical components.
Conclusion:
The incorrect statement is that both projectiles will have the same range. This is because the ranges depend on both the horizontal and vertical components of the velocities, and while the horizontal components are equal, the vertical components may not be.
Final Answer:
The incorrect statement is: "Both projectiles will have the same range."
- Two projectiles are thrown simultaneously from the same point.
- Their velocities are v1 and v2 at angles θ1 and θ2 respectively.
- It is given that v1cosθ1=v2cosθ2.
Identify the incorrect statement based on the given conditions.
The condition v1cosθ1=v2cosθ2 indicates that the horizontal components of the velocities of both projectiles are equal. This means both projectiles will have the same horizontal displacement over time.
The vertical components of the velocities are given by v1y=v1sinθ1 and v2y=v2sinθ2. The time of flight for each projectile can be calculated using the vertical motion equations, which depend on the vertical components of their velocities.
Since the horizontal components are equal, we can conclude that if the time of flight is the same, the horizontal distance covered will also be the same. However, the time of flight may not necessarily be the same unless the vertical components are also equal.
The maximum height attained by each projectile can be calculated using the vertical components. If the vertical components are equal, then the maximum heights will also be equal.
Since the horizontal components are equal, the trajectory of one projectile with respect to the other will appear as a vertical straight line when viewed from the frame of reference of one of the projectiles.
The statements can be analyzed:
- If the horizontal components are equal, the trajectories will be vertical lines.
- The time of flight is not guaranteed to be the same unless the vertical components are also equal.
- The maximum heights can be equal if the vertical components are equal.
The incorrect statement is that both projectiles will have the same range. This is because the ranges depend on both the horizontal and vertical components of the velocities, and while the horizontal components are equal, the vertical components may not be.
The incorrect statement is: "Both projectiles will have the same range."
Similar Questions
Two projectivles are thrown simultaneously in the same plane from the same point. Iff their velocities are v1andv2 at angles θ1andθ2 respectively from the horizontal, then answer the following questions.
Q. If v1=v2andθ1>θ2, then choose the incorrect statementView SolutionTwo projectiles are thrown simultaneously in the same plane from the same point. If their velocities are v1 and v2 at angles θ1 and θ2 respectively from the horizontal, then ansewer the following questions
The trajectory of particle 1 with respect to particle 2 wil beView Solution
Knowledge Check
- Question 1 - Select One
Two projectiles are thrown simultaneously in the same plane from the same point. If their velocities are v1 and v2 at anglesθ1 and θ2 respectively from the horizontal, then answer the following questions.
If v1cosθ1=v2cosθ2, then choose the incorrect statementAone particle will remain exactly below or above the other particleBthe trajectory of one with respect to other will be a vertical straight lineCboth will have the same rangeDnone of these - Question 2 - Select One
Two projectivles are thrown simultaneously in the same plane from the same point. Iff their velocities are v1andv2 at angles θ1andθ2 respectively from the horizontal, then answer the following questions.
Q. If v1sinθ1=v2sinθ2, then choose the incorrect statementAThe time of flight of both the particles will be sameBThe maximum height attained by the particles will be sameCThe trajectory of one with respect to another will be a horizontal straight lineDNone of these - Question 3 - Select One
Two projectivles are thrown simultaneously in the same plane from the same point. Iff their velocities are v1andv2 at angles θ1andθ2 respectively from the horizontal, then answer the following questions.
Q. If v1=v2andθ1>θ2, then choose the incorrect statementAParticle 2 moves under the particle 1BThe slope of the trajectory of particle 2 with respect to 1 is always positiveCBoth the particle will have the same range if θ1>45∘andθ2<45∘andθ1+θ2=90∘Dnone of these
Two particles are projected simultaneously in the same vertical plane from the same point, with different speeds u1 and u2, making angles θ1 and θ2 respectively with the horizontal, such that u1cosθ1=u2cosθ2. The path followed by one, as seen by the other (as long as both are in flight), is
View SolutionTwo balls are projected simultaneously in the same vertical plane from the same point with velocities v1 and v2 with angle θ1 and θ2 respectively with the horizontal. If v1 cos θ1=v2cosθ2, the path of one ball as seen from the position of other ball is :
View SolutionTwo particles are projected simultaneously in the same vertical plane, from the with speed u1 and u2 at angle of projection θ1 and θ2 respectively with the horizontal. The path followed by one, as seen by other (as long as both are in flight), is
View SolutionTwo particles are projected simultaneously in the same vertical plane from the same point, with different speeds u1 and u2, making angles θ1 and θ2 respectively with the horizontal, such that u1cosθ1=u2cosθ2. The path followed by one, as seen by the other (as long as both are in flight), is
View SolutionTwo particles of equal mass in are projected from the ground with speeds v1 and v2 at angles θ1, and θ2 as shown in the figure. Given θ2>θ1 and v1cosθ1=v2cosθ2Which statement/s is/are correct?
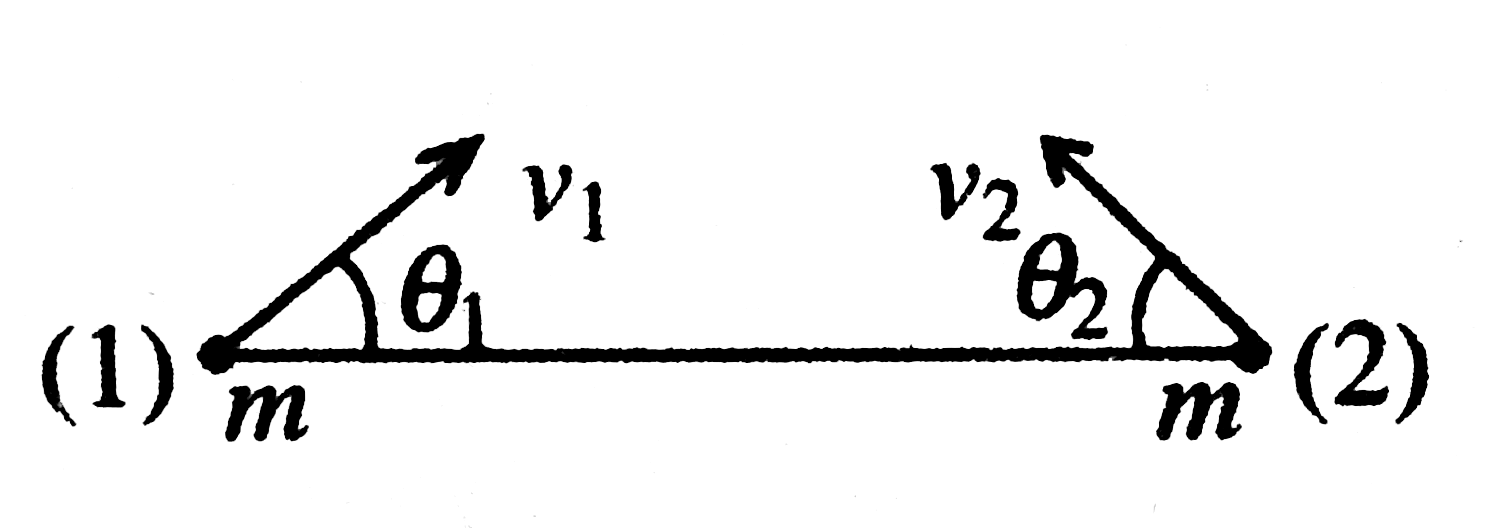 View Solution
View Solution

