STATEMENT-1: Two balls are dropped one after the other form a tall tower. The distance between them increases linearly with time (elapsed after the second ball is dropped and before the first hits ground).
STATEMENT-2: Relative acceleration is zero, whereas relative velocity non-zero in the above situation.
Statement -1 is True, Statement-2 is Ture, Statement-2 is a correct explanantion for Statement-1.
Statement-1 is Ture, Statement-2 is Ture, Statement-2 is Not a correct explanantion for Statement-1.
Statement-1 is True, Statement-2 is False.
Statement-1 is False, Statement-2 is True.
The correct Answer is:A
To solve the problem, we need to analyze the two statements provided and determine their validity based on the principles of kinematics.
1. Understanding the Scenario:
- Two balls are dropped from a tower: the first ball is dropped at time t=0 and the second ball is dropped at time t=t0 (where t0 is some positive time after the first ball).
- We need to analyze the motion of both balls and the distance between them after the second ball is dropped until the first ball hits the ground.
2. Motion of the First Ball:
- The first ball is in free fall with an initial velocity u1=0 and an acceleration a1=g (acceleration due to gravity).
- The distance fallen by the first ball after t1 seconds (where t1 is the time since it was dropped) is given by:
y1=12gt21
3. Motion of the Second Ball:
- The second ball is also in free fall with an initial velocity u2=0 and an acceleration a2=g.
- The time of fall for the second ball after it is dropped is t2=t−t0 (where t is the total time since the first ball was dropped).
- The distance fallen by the second ball is:
y2=12g(t−t0)2
4. Distance Between the Two Balls:
- The distance D between the two balls after the second ball is dropped can be expressed as:
D=y1−y2=12gt21−12g(t−t0)2
- Since t1=t−t0, we can substitute this into the equation:
D=12g(t−t0)2−12g(t−t0)2=12g(t0)(2(t−t0))=g(t0)(t−t0)
- This shows that the distance D increases linearly with time t.
5. Relative Acceleration and Velocity:
- Both balls experience the same acceleration g downwards. Therefore, their relative acceleration is:
arel=a1−a2=g−g=0
- The relative velocity vrel is non-zero because the first ball has a velocity that increases with time, while the second ball starts from rest:
vrel=v1−v2=gt1−0=gt1
6. Conclusion:
- Statement 1 is true: The distance between the two balls increases linearly with time.
- Statement 2 is also true: The relative acceleration is zero, while the relative velocity is non-zero.
Final Answer:
Both statements are correct, and Statement 2 is the correct explanation of Statement 1. Thus, the answer is A.
---
- Two balls are dropped from a tower: the first ball is dropped at time t=0 and the second ball is dropped at time t=t0 (where t0 is some positive time after the first ball).
- We need to analyze the motion of both balls and the distance between them after the second ball is dropped until the first ball hits the ground.
- The first ball is in free fall with an initial velocity u1=0 and an acceleration a1=g (acceleration due to gravity).
- The distance fallen by the first ball after t1 seconds (where t1 is the time since it was dropped) is given by:
y1=12gt21
- The second ball is also in free fall with an initial velocity u2=0 and an acceleration a2=g.
- The time of fall for the second ball after it is dropped is t2=t−t0 (where t is the total time since the first ball was dropped).
- The distance fallen by the second ball is:
y2=12g(t−t0)2
- The distance D between the two balls after the second ball is dropped can be expressed as:
D=y1−y2=12gt21−12g(t−t0)2
- Since t1=t−t0, we can substitute this into the equation:
D=12g(t−t0)2−12g(t−t0)2=12g(t0)(2(t−t0))=g(t0)(t−t0)
- This shows that the distance D increases linearly with time t.
- Both balls experience the same acceleration g downwards. Therefore, their relative acceleration is:
arel=a1−a2=g−g=0
- The relative velocity vrel is non-zero because the first ball has a velocity that increases with time, while the second ball starts from rest:
vrel=v1−v2=gt1−0=gt1
- Statement 1 is true: The distance between the two balls increases linearly with time.
- Statement 2 is also true: The relative acceleration is zero, while the relative velocity is non-zero.
Both statements are correct, and Statement 2 is the correct explanation of Statement 1. Thus, the answer is A.
Similar Questions
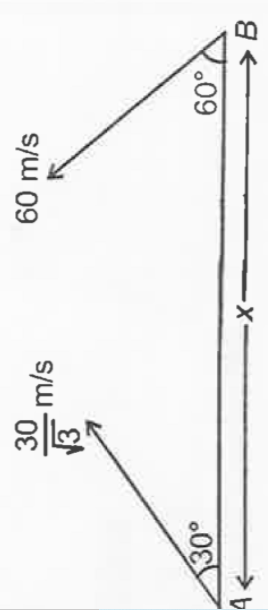
Two balls are projected from two points A and B,x metre apart as shown in figure.The time after which the horizontal distance between them become zero is
 View Solution
View SolutionA second ball is dropped down from an elevator acceleration up with 1m/s2, 1 second after the first ball is dropped. How does the relative velocity of the two balls change with time. How the ratio v1/v2 change with time.
View Solution
Knowledge Check
- Question 1 - Select One
A ball is dropped downwards. After 1 second another ball is dropped downwards from the same point. What is the distance between them after 3 seconds
A25mB20mC50mD9.8m - Question 2 - Select One
From a balloon rising vertically with uniform acceleration f a ball is dropped, 4 seconds after this another ball is dropped from the balloon. The distance. between the two balls 2 seconds after the second ball is dropped is
A16 (g+f)B10 (g+f)C8 (g+f)DNone - Question 3 - Select One
A ball is dropped downwards . After 1 second another ball is dropped downwards from the same point . What is the distance between them after 3 seconds .
A20 mB9.8mC25 mD50 m
STATEMENT 1 : Two stones are projected with different velocities from ground from same point and at same instant of time. Then these stones cannot collide in mid air. (Neglect air friction) STATEMENT 2 : If relative acceleration of two particles initially at same position is always zero, then the distance between the particle either remains constant or increases continuously wiht time.
View SolutionFour marbles are dropped from the top of a tower one after the other with an interval of one second. The first one reaches the ground after 4 seconds . When the first one reaches the ground the distance between the first and second, the second and third and the third and forth will be respectively
View SolutionTwo balls are dropped from the same point after an interval of 1s. If acceleration due to gravity is 10m/s2, what will be their separation 3 seconds after the release of first ball?
View SolutionA body is thrown up with a velocity 40ms−1. At same time another body is dropped from a height 40 m. Their relative acceleration after 1.3 seconds is
View SolutionTwo balls of same mass are dropped from the same height h, on to the floor. The first ball bounces to a height h/4, after the collision & the second ball to a height h/16. The impulse applied by the first & second ball on the floor are I1 and I2 respectively. Then
View Solution

