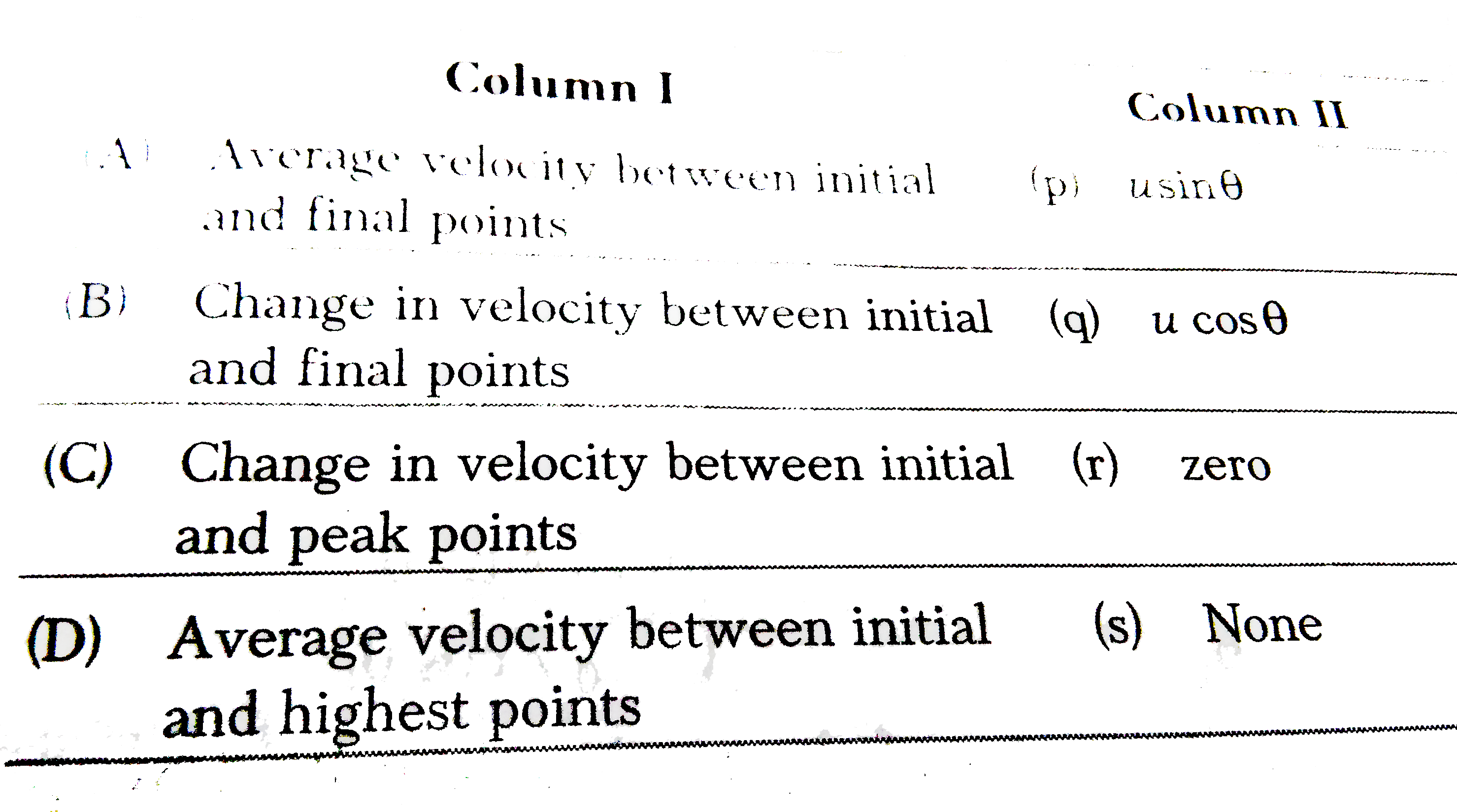STATEMENT-1: A particle si projected at an angle θ(<90) to horizontal, with a velcotiy u. When particle strikes the ground its speed is again u.
STATEMENT-2: Velocity along horizontal direction remains same but velocity along vertical direction is changed. When particle strikes the ground, magnitude of final vertical velocity is equal to magnitude of initla vertical velocity.
Statement -1 is True, Statement-2 is Ture, Statement-2 is a correct explanantion for Statement-1.
Statement-1 is Ture, Statement-2 is Ture, Statement-2 is Not a correct explanantion for Statement-1.
Statement-1 is True, Statement-2 is False.
Statement-1 is False, Statement-2 is True.
The correct Answer is:A
(Ux=0ax=0,,⇒,Vx=Ux+axT=Ux,),(Uy=usinθ,ay=−g,,⇒,Vy=usinθ−gt,)
=usinθ−g.2usinθg,Vy=−usinθ.
Similar Questions
Knowledge Check
- Question 1 - Select One
When a projectile is fired at an angle θ w.r.t horizontal with velocity u, then its vertical component:
Aremains sameBgoes on increasing with heightCgoes on decreasing with heightDfirst increase then decreases with height - Question 2 - Select One
Assertion: In projectile motion horizontal velocity remains same but vertical velocity continously change and particle strikes the ground with same vertical velocity with which the particle was thrwon in vertical direction.
AIf both assertion & Reason are True & the Reason is a corrrect explanation of the Asserion.BIf both Assertion & Reason are True but Reason is not correct explanation of the Assertion.CIf Assertion is Trie but the Reason is False.DIf both Assertion & Reason are false - Question 3 - Select One
A projectill is projected at an angle (α>45∘) with an initial velocity u. The time t, at which its magnitude of horizontal velocity will equal the magnitude of vertical velocity is :-
At=ug(cosα−sinα)Bt=ug(cosα+sinα)Ct=ug(sinα−cosα)Dt=ug(sin2α−cos2α)
A particle is fired with velocity u making angle θ with the horizontal.What is the change in velocity when it is at the highest point?
View SolutionA particle is projected with a speed u at an angle θ with the horizontal. What will be the speed of the particle when direction of motion of particle is at an angle α with the horizontal?
View SolutionA particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
View SolutionA particle projected with velocity u at angle θ with horizontal at t=0. What is the magnitude of change in the velocity of the particle when it is at maximum height?
View SolutionA particle is projected with speed 'u' at an angle 60∘ with horizontal, then find the speed when its angle with horizontal changes to 30∘ .
View Solution