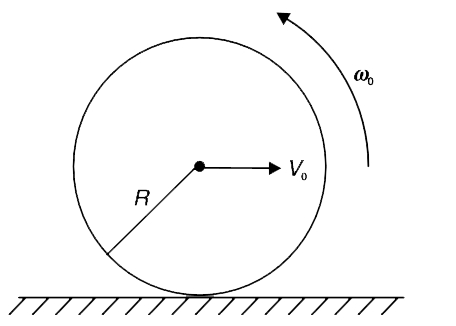
A sphere of mass M and radius r shown in figure slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre v02r. Find the translational velocity after the sphere starts pure rolling.
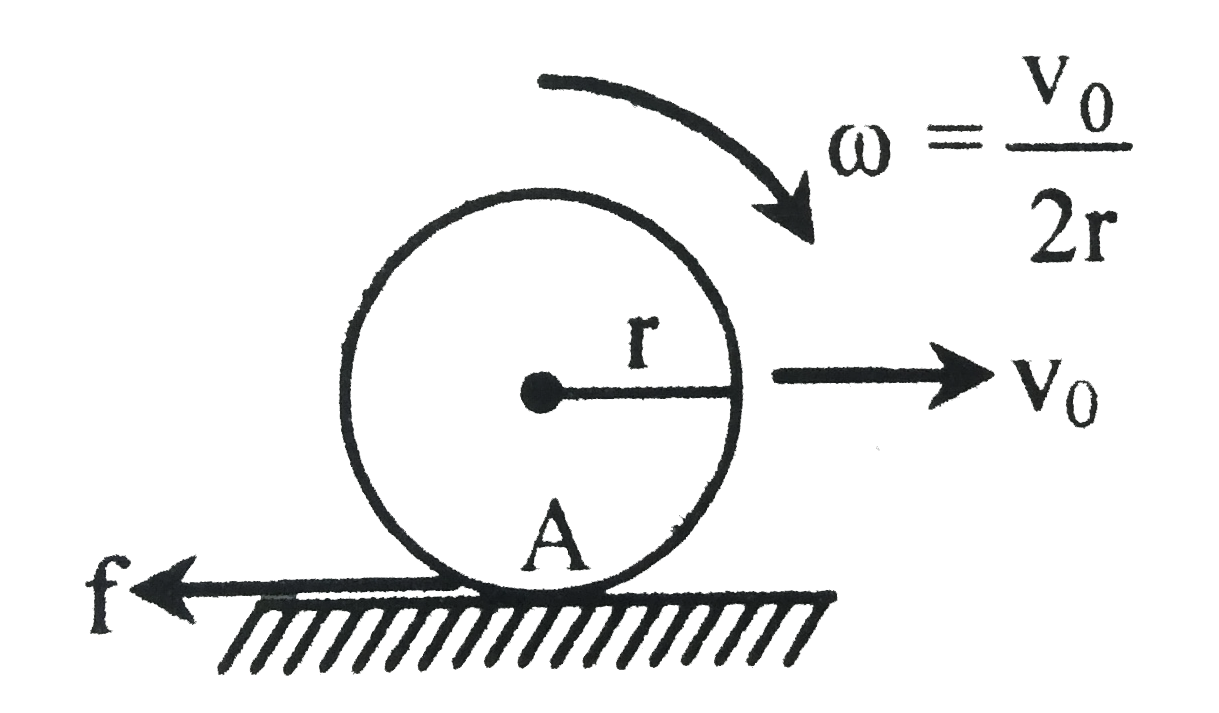 .
.
Velocity of the centre = V0 and the angular velocity about the centre =v02r. Thus v0>ω0r.
The sphere slips forward and thus the friction by the plane on the sphere will act backward. As the friction is kinetic, its value is μN=μMg and the sphere will be decelerated by acm=f/M. Hence
v(t)=v0−fMt. ....(i)
This friction will also have a torque Γ about the centre. This torque is clockwise and in the direction of ω0. Hence the angular acceleration about the centre will be
α=f(r)(2/5)Mr2=5f2Mr
and the clockwise angular velocity at time t will be
ω(t)=ω0+5f2Mrt=v02r+5f2Mrt.
Pure rolling starts when v(t)=rω(t)
i.e., v(t)=v02+5f2Mt. ....(ii)
Eliminating t from (i) and (ii),
52v(t)+v(t)=52V0+v02
or v(t)=27×3V0=67V0
Thus, the sphere rolls with translational velocity 6v0/7 in the forward direction.
Similar Questions
A sphere of mass M and radius r shown in figure slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre v02r. Find the translational velocity after the sphere starts pure rolling.
 .View Solution
.View SolutionA solid sphere of mass M and radius r slips on a rough horizontal plane. At some instant it has translational velocity v0androtationalvelocityaboutthecentrev_(0) / 2 r.Thetranslationalvelocityafterthesphere⋆tspureroll∈gis(x v_(0))/(y)∈forwarddirection.F∈d(x+y).
'(##CEN_KSR_PHY_JEE_C09_E01_027_Q14##)'View Solution
Knowledge Check
- Question 1 - Select One
A sphere of mass M and radius r shown in the figure on a rough horizontal plane. At some instant it has translational velocity v0, and rotational velocity about centre v0/2r. The percentage change of translational velocity after the sphere start pure rolling:
 A14.28%B7.14%C21.42%Dnone
A14.28%B7.14%C21.42%Dnone - Question 2 - Select One
A sphere of mass M and radius r slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre V02r. The translational velocity when the sphere starts pure rolling motion is
AV05BV07CV03D6V07 - Question 3 - Select One or More
A wheel is rolling on a horizontal plane. At a certain instant it has a velocity v and acceleration a of CM as shown in figure . Acceleration of
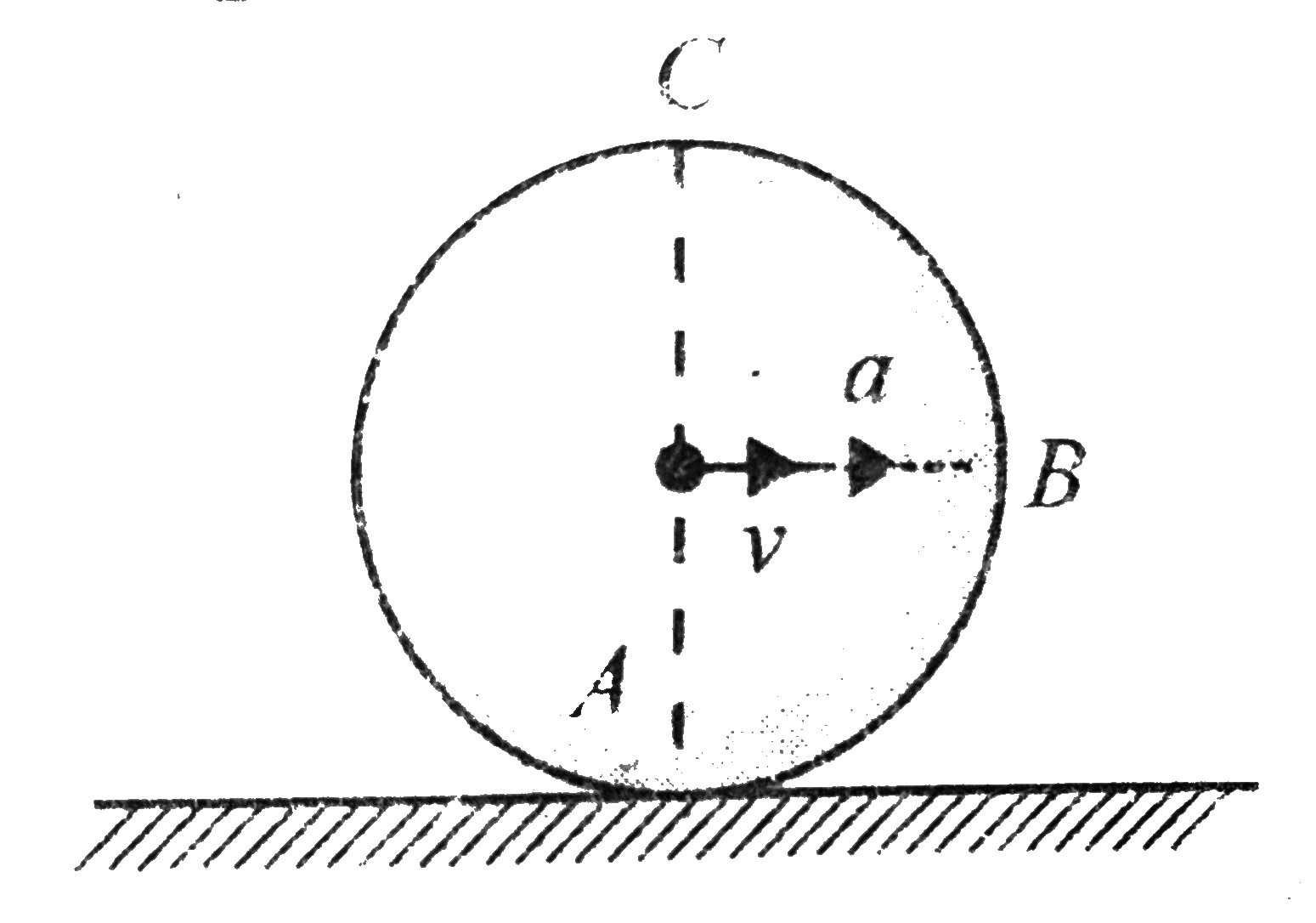 AA is vertically upwardsBB may be vertically down-wardsCC cannot be horizontalDsome point on the rim may he horizontal leftwards
AA is vertically upwardsBB may be vertically down-wardsCC cannot be horizontalDsome point on the rim may he horizontal leftwards
Consider a hollow sphere rolling with slipping with velocities as shown. Find the translational velocity after the hollow sphere starts pure rolling.
(a)
(b)
(c ) View Solution
View Solution(i) A solid sphere of radius R is released on a rough horizontal surface with its top point having thrice the velocity of its bottom point A (VA=V0) as shown in figure. Calculate the linear velocity of the centre of the sphere when it starts pure rolling.
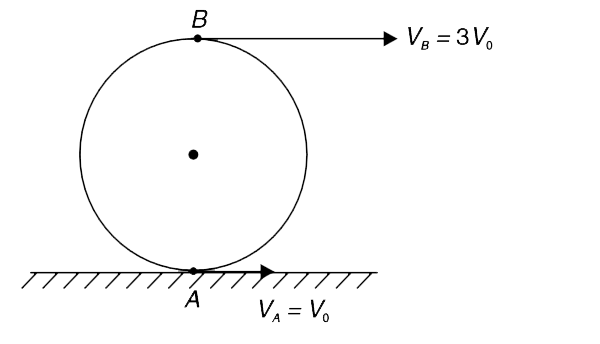
(ii) Solid sphere of radius R is placed on a rough horizontal surface with its centre having velocity V0 towards right and its angular velocity being ω0 (in anticlockwise sense). Find the required relationship between V0 and ω0 so that -
(a) the slipping ceases before the sphere loses all its linear momentum.
(b) the sphere comes to a permanent rest after some time.
(c) the velocity of centre becomes zero before the spinning ceases.View SolutionA uniform solid sphere of mass m and radius r = 3m is projected along a rough horizontal surface with the initial velocity v0=6m/s and angular ω0 velocity as shown in the figure. If the sphere finally comes to complete rest then angular velocity is x rad/s. Find x.
 View Solution
View SolutionA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
View SolutionA ring of mass m and radius R is rolling on a horizontal plane. If the ring suddenly starts rotating about its diameter, then its angular velocity in this will be
View Solution

