A uniform ladder of length $l$ rests against a smooth, vertical wall (figure). If the mass of the ladder is $m$ and the the coefficient of static friction between the ladder and the ground is $μ_{s} = 0.375$ and the minimum angle $θ_{min}$ at which the ladder does not slip.

A uniform ladder at rest, leading against a smooth wall. Th ground is rough.

Video Solution

Text Solution

Verified by Experts

Applying the first condition for equilinrium to the ladder, we have
(1) $Σ F_{x} = f_{s} - P = 0$
(2) $Σ F_{y} = n - m g = 0$
The first equation tells us that $P = f_{0}$ . From the second equation we see that n $= m g$ . Furthermore, when the ladder is on the verge of slipping, the force of friction must be a mximum, which is given by $f_{c, max} = μ_{s} n = μ_{s} m g$ .
The find $θ_{min}$ , we must use the second condition for equilibrium. When we take the torque about an axis through the origin $O$ at the bottom of the ladder, we have
$Σ τ_{0} = P l sin θ - (m g) \frac{l}{2} cos θ = 0$
This expression gives
${tan θ}_{min} = \frac{m g}{2 P} = \frac{m g}{2 μ_{s} m g} = \frac{1}{2 μ_{s}} = 1.25$
$θ_{min} = 53^{\circ}$ .
Any body experiencing zero net force & zero torque about $C . M$ is raid to be in equilibrium.

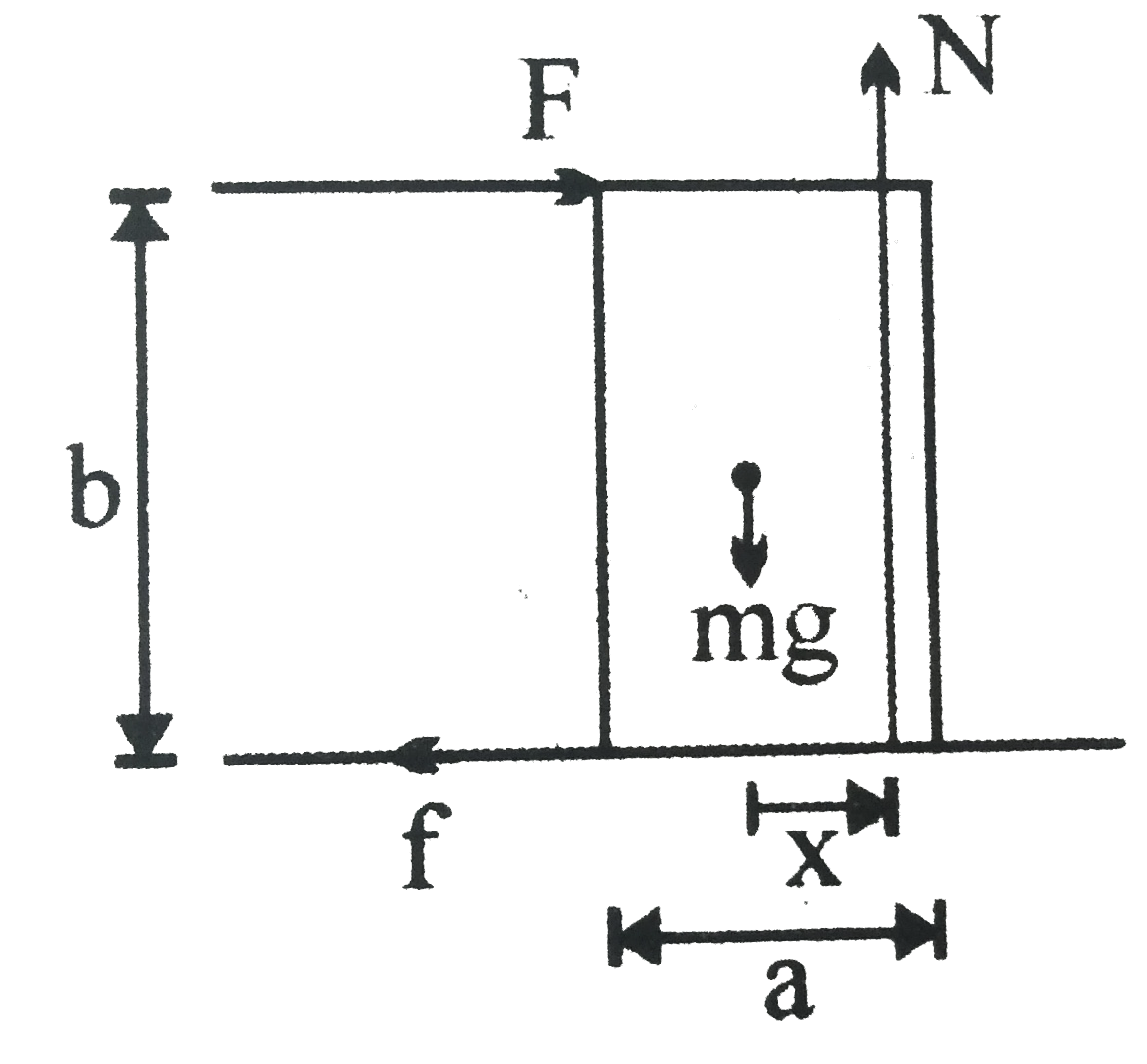
$F \frac{1}{2} + \frac{f (1)}{2} - N x = 0$
$N = m g, F = f$
$x = \frac{F b}{N} = \frac{F b}{m g}$
but $x < \frac{a}{2}$
for not toppling $\frac{a}{2} > \frac{F b}{m g}$ or $\frac{a}{2 b} > \frac{F}{m g}$
assuming $F < μ m g$ .

Updated on:21/07/2023

A ladder of length $l$ and mass $m$ is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is $μ$ . The angle $θ$ at which the ladder will stay in equilibrium is
A $θ = {tan}^{- 1} (μ)$
B $θ = {tan}^{- 1} (2 μ)$
C $θ = {tan}^{- 1} (\frac{μ}{2})$
Dnone of these
A ladder of length $5 m$ is placed against a smooth wall as shown in figure. The coefficient or friction is $μ$ between ladder and ground. What is the minimum value of $μ$ , If the ladder is not to slip?

A $μ = \frac{1}{2}$
B $μ = \frac{1}{4}$
C $μ = \frac{3}{8}$
D $μ = \frac{5}{8}$
A uniform ladder $5.0 m$ long rests against a frictionless, vertical wall with its lower end $3.0 m$ to from the wall. The ladder weighs $160 N$ . The coefficient of static friction between the foot of the ladder and the ground is $0.40$ . A man weighing $740 N$ climbs slowly up the ladder.
How far along the ladder can the man climb before the ladder starts to slip?
A $3 m$
B $5 m$
C $2.7 m$
D $1.25 m$