Two uniform spheres of mass M have radii R and 2R. Each sphere is rotating about a fixed axis through a diameter, the rotational kinetic energies of the sphere are identical. What is the ratio of the magnitude of the angular momentum of these spheres gt That is, L2RLR=
A
4
B
2√2
C
2
D
√2
Video Solution
Text Solution
The correct Answer is:C
KE=L22I
L=√2I(K.E)⇒L2RLR=√I2RIR=
⎷25×m(2R)225mR2
L2RLR=21.
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
The radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of this axis from the centre of the sphere is
ArB0.5 rC√0.6rD√0.4r - Question 2 - Select One
A solid sphere of mass M and radius R spins about an axis passing through its centre making 600 r.p.m. What is its kinetic energy of rotation?
A25πM2R2B80π2MR2C80πRD25π2MR - Question 3 - Select One
Two flywheels of the same mass have radius R and r where R>r, and they have same rotational kinetic energy then the angular momentum (L) is more for
Agreater radius wheelBlesser radius wheelCboth with have same LDdepends upon shape L
The radius of gyration of a uniform solid sphere of radius R., about an axis passing through a point R2 away from the centre of the sphere is:
View SolutionInside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
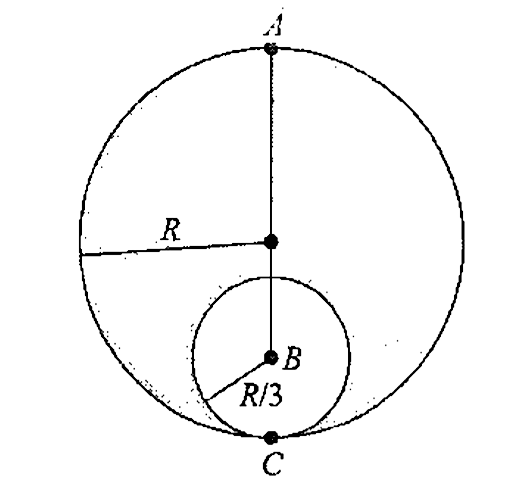 View Solution
View SolutionAngular momentum L and rotational kinetic energy KR of a body are related to each other by the relation. (I = moment of inertia)
View SolutionA solid sphere is rolling without slipping on a horizontal plane. The ratio of its rotational kinetic energy and translational kinetic energy is
View SolutionA solid sphere of mass M and radius R spins about an axis passing through its centre making 600 rpm. Its kinetic energy of rotation is
View Solution

