A mass m is moving at speed v perpendicular to a rod of length d and mass M=6m pivots around a frictionless axle running through its centre and stickes to the end of the rod. The moment of inertia od the rod about its centre is Md2/12. Then the angular speed of the system right after the collision us -
2v/d
2v/(3d)
v/d
3v/(2d)
The correct Answer is:B

From conservation of angular momentum
J=Iω
d2×mv=[Md212+m(d2)2]ω
mvd2=[6md212+md24]ω
mvd2=3md2ω4
ω=2v3d.
Similar Questions
A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
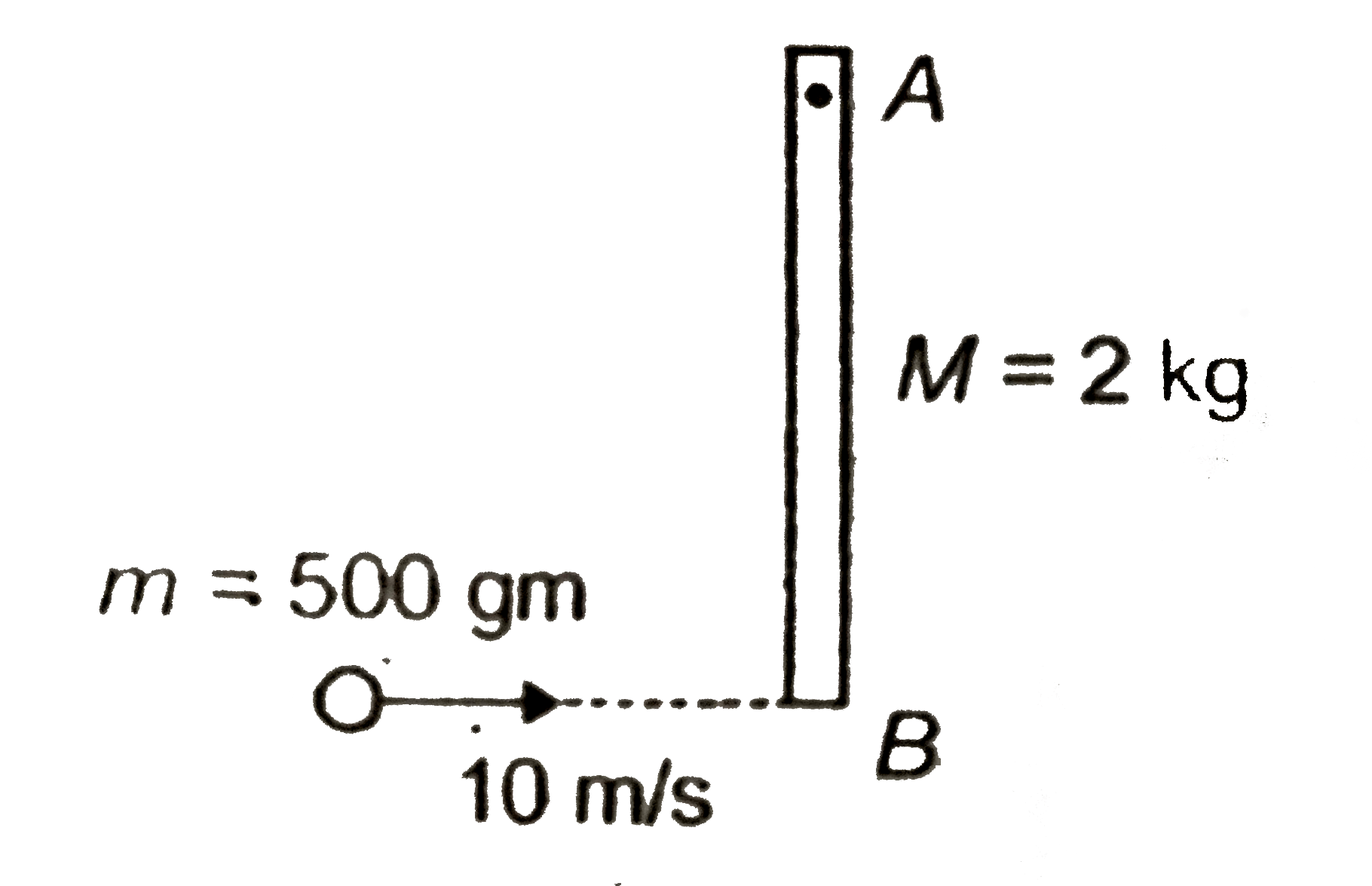
View SolutionA rod of mass 2kg and length 1m is pivoted at one end A and kept on a smooth surface. A particle of mass 500gmstrikestheotherendB of the rod and sticks to the rod. If particle was moving with the speed of 20m/s, what is the angular speed of the rod after collision ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A rod of length 2 m has a mass of 0.24 kg. Its moment of inerita about an axis passing through its centre and perpendicular to the length of the rod is
A0.04 kg - m2B0.08 kg - m2C0.12 kg - m2D0.02 kg - m2 - Question 2 - Select One
The moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an angle α is
 Aml23sin2αBml212sin2αCml22cos2αDml22cos2α
Aml23sin2αBml212sin2αCml22cos2αDml22cos2α - Question 3 - Select One
The moment of inertia of a thin uniform rod of mass M and length l about an axis perpendicular to the rod through its centre is I. The moment of inertia of the rod through its end point is
AI4BI2C2ID4I
A rod of length 2 m, has a mass of 0.12 kg. Its moment of inertia about an axis passing through its one end and perpendicular to the length of the rod is
View SolutionMoment of inertia of a rod of mass m and length l about its one end is l. If one-fourth of its length is cur away, then moment of inertia of the remaining rod about its one end will be
View SolutionMoment of inertia of a uniform rod of length L and mass M, about an axis passing through L/4 from one end and perpendicular to its length is
View SolutionMoment of inertia of a uniform rod of length L and mass M , about an axis pasing through L/4 from one end and perpendicular to its length is
View SolutionThe moment of inertia of a thin uniform rod of mass M and length L about an axis perpendicular to the rod, through its centre is I. The moment of inertia of the rod about an axis perpendicular to rod through its end point is
View Solution

